题目内容
17.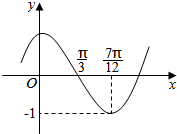 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0≤φ<2π)的部分图象如图所示
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0≤φ<2π)的部分图象如图所示 (1)写出函数f(x)的最小正周期及解析式(不要求解题过程)
(2)将函数f(x)的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数y=g(x)的图象.求函数g(x)的单调递增区间.
分析 (1)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数f(x)的解析式.
(2)由条件利用y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,再利用正弦函数的增区间求得函数g(x)的增区间.
解答 解:(1)由函数f(x)=Asin(ωx+φ)的部分图象可得A=1,再根据$\frac{T}{4}$=$\frac{1}{4}$×$\frac{2π}{ω}$=$\frac{7π}{12}$-$\frac{π}{3}$,求得ω=2,最小正周期T=π.
再根据五点法作图可得2×$\frac{π}{3}$+φ=π,求得φ=$\frac{π}{3}$,∴函数f(x)=sin(2x+$\frac{π}{3}$).
(2)把f(x)=sin(2x+$\frac{π}{3}$)的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数y=g(x)=sin(x+$\frac{π}{3}$)的图象,
令2kπ-$\frac{π}{2}$≤x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,求得2kπ-$\frac{5π}{6}$≤x≤2kπ+$\frac{π}{6}$,
可得函数g(x)的增区间为[2kπ-$\frac{5π}{6}$,2kπ+$\frac{π}{6}$],k∈Z.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值;y=Asin(ωx+φ)的图象变换规律,正弦函数的增区间,属于中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
5.设f(x)=2x+3,g(x)=f(x-2),则g(x)等于( )
| A. | 2x+1 | B. | 2x-1 | C. | 2x-3 | D. | 2x+7 |