题目内容
设x1、x2是函数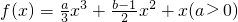 的两个极值点.
的两个极值点.
(1)若x1<2<x2<4,求证:f′(-2)>3;
(2)如果|x1|<2,|x2-x1|=2,求b的取值范围;
(3)如果a≥2,且x2-x1=2,x∈(x1,x2)时,求函数g(x)=|f′(x)+2(x-x2)|的最大值h(a).
解:由已知:f'(x)=ax2+(b-1)x+1
故x1,x2是方程f'(x)=0的两根
(1)由于x1<2<x2<4故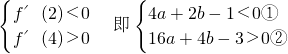 由于f'(-2)=4a-2b+3
由于f'(-2)=4a-2b+3
①×(-3)+②得:4a-2b>0
∴f'(-2)>3
(2)由韦达定理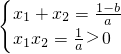
故1-b=
当0<x1<2时,则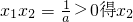 >0
>0
这时,由|x2-x1|=2得x2=x1+2
即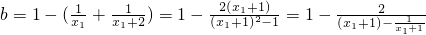 为增函数(也可用求导法来证),
为增函数(也可用求导法来证),
故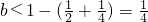
当-2<x1<0时,有x1-x2=2,则b=1-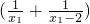 也为增函数
也为增函数
故这时,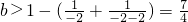
综上,b的取值范围是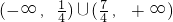
(3)∵a≥2,x2-x1=2故可设f'(x)=a(x-x1)(x-x2)
∴g(x)=|f'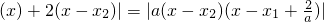
∵x∈(x1,x2)∴x-x2<0,x-x1>0,x-x1+ >0
>0
∴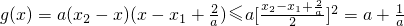 +2
+2
当且仅当x2-x=x-x1+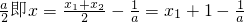 等号成立.
等号成立.
∴h(a)=a+ +2a∈[2,+∞).
+2a∈[2,+∞).
分析:(1)利用导数与函数极值的关系列出关于a,b的不等式组是解决本题的关键,利用整体思想确定出f′(-2)的取值范围;
(2)建立b与x1,x2的关系是解决本题的关键.根据所得的函数表达式利用函数的单调性求出b的取值范围;
(3)写出函数g(x)的表达式是解决本题的关键,根据基本不等式求出函数的最大值h(a).
点评:此题是个难题.本题属于函数与不等式的综合问题,利用导数的基本知识确定出相关的关系,列出相关的不等式进行综合转化.本题考查学生的转化与化归思想,考查不等式的基本方法和技巧.考查导数的工具作用.
故x1,x2是方程f'(x)=0的两根
(1)由于x1<2<x2<4故
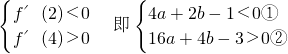 由于f'(-2)=4a-2b+3
由于f'(-2)=4a-2b+3①×(-3)+②得:4a-2b>0
∴f'(-2)>3
(2)由韦达定理
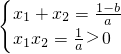
故1-b=

当0<x1<2时,则
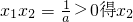 >0
>0这时,由|x2-x1|=2得x2=x1+2
即
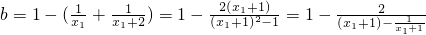 为增函数(也可用求导法来证),
为增函数(也可用求导法来证),故
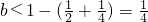
当-2<x1<0时,有x1-x2=2,则b=1-
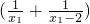 也为增函数
也为增函数故这时,
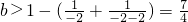
综上,b的取值范围是
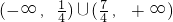
(3)∵a≥2,x2-x1=2故可设f'(x)=a(x-x1)(x-x2)
∴g(x)=|f'
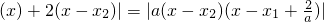
∵x∈(x1,x2)∴x-x2<0,x-x1>0,x-x1+
 >0
>0∴
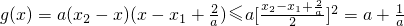 +2
+2当且仅当x2-x=x-x1+
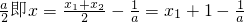 等号成立.
等号成立.∴h(a)=a+
 +2a∈[2,+∞).
+2a∈[2,+∞).分析:(1)利用导数与函数极值的关系列出关于a,b的不等式组是解决本题的关键,利用整体思想确定出f′(-2)的取值范围;
(2)建立b与x1,x2的关系是解决本题的关键.根据所得的函数表达式利用函数的单调性求出b的取值范围;
(3)写出函数g(x)的表达式是解决本题的关键,根据基本不等式求出函数的最大值h(a).
点评:此题是个难题.本题属于函数与不等式的综合问题,利用导数的基本知识确定出相关的关系,列出相关的不等式进行综合转化.本题考查学生的转化与化归思想,考查不等式的基本方法和技巧.考查导数的工具作用.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
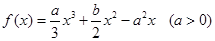 的两个极值点,且
的两个极值点,且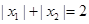 。
。 ,并求出a的取值范围.
,并求出a的取值范围.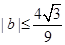 .
.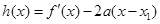 ,证明:当
,证明:当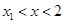 且x1<0时,
且x1<0时, 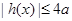 .
.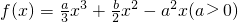 的两个极值点,且|x1|+|x2|=2.
的两个极值点,且|x1|+|x2|=2.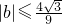 .
.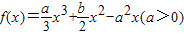 的两个极值点,且|x1-x2|=2.
的两个极值点,且|x1-x2|=2. .
.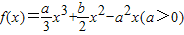 的两个极值点,且|x1-x2|=2.
的两个极值点,且|x1-x2|=2.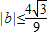 .
.