题目内容
已知椭圆的中心是坐标原点O,焦点在x轴上,离心率为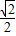 ,又椭圆上任一点到两焦点的距离和为
,又椭圆上任一点到两焦点的距离和为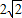 ,过点M(0,
,过点M(0,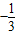 )与x轴不垂直的直线l交椭圆于P、Q两点.
)与x轴不垂直的直线l交椭圆于P、Q两点.(1)求椭圆的方程;
(2)在y轴上是否存在定点N,使以PQ为直径的圆恒过这个点?若存在,求出N的坐标,若不存在,说明理由.
【答案】分析:(1)由椭圆定义可知2a=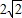 ,由此可得a值,再由离心率可得c值,由a2=b2+c2可求b值;
,由此可得a值,再由离心率可得c值,由a2=b2+c2可求b值;
(2)设l的方程为y=kx- ,P(x1,y1),Q(x2,y2),假设在y轴上存在定点N(0,m)满足题设,则对于任意的k∈R,
,P(x1,y1),Q(x2,y2),假设在y轴上存在定点N(0,m)满足题设,则对于任意的k∈R,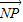 •
• =0恒成立,联立直线l与椭圆方程,消掉y得x的方程,由韦达定理及向量的数量积运算可把
=0恒成立,联立直线l与椭圆方程,消掉y得x的方程,由韦达定理及向量的数量积运算可把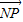 •
• =0化为关于k的恒等式,从而可得m的方程组,解出即可.
=0化为关于k的恒等式,从而可得m的方程组,解出即可.
解答:解:(1)因为离心率为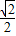 ,又2a=
,又2a=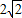 ,∴a=
,∴a=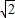 ,c=1,故b=1,故椭圆的方程为
,c=1,故b=1,故椭圆的方程为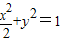 ;
;
(2)设l的方程为y=kx- ,
,
由 得(2k2+1)x2-
得(2k2+1)x2- kx-
kx-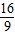 =0,
=0,
设P(x1,y1),Q(x2,y2),则x1+x2=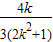 ,x1•x2=
,x1•x2=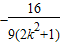 ,
,
假设在y轴上存在定点N(0,m)满足题设,则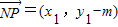 ,
,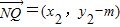 ,
,
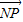 •
•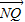 =x1x2+(y1-m)(y2-m)=x1x2+y1y2-m(y1+y2)+m2
=x1x2+(y1-m)(y2-m)=x1x2+y1y2-m(y1+y2)+m2
=x1x2+(kx1- )( kx2-
)( kx2- )-m(kx1-
)-m(kx1- +kx2-
+kx2- )+m2
)+m2
=(k2+1)x1x2-k( +m)•(x1+x2)+m2+
+m)•(x1+x2)+m2+ m+
m+
=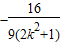 -k(
-k( +m)•
+m)• +m2+
+m2+ m+
m+
=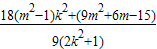 ,
,
由假设得对于任意的k∈R, •
• =0恒成立,即
=0恒成立,即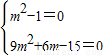 ,解得m=1,
,解得m=1,
因此,在y轴上存在定点N,使得以PQ为直径的圆恒过这个点,点N的坐标为(0,1).
点评:本题考查直线与圆锥曲线的位置关系及椭圆方程的求解,考查向量的有关运算,考查学生分析解决问题的能力.
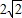 ,由此可得a值,再由离心率可得c值,由a2=b2+c2可求b值;
,由此可得a值,再由离心率可得c值,由a2=b2+c2可求b值;(2)设l的方程为y=kx-
 ,P(x1,y1),Q(x2,y2),假设在y轴上存在定点N(0,m)满足题设,则对于任意的k∈R,
,P(x1,y1),Q(x2,y2),假设在y轴上存在定点N(0,m)满足题设,则对于任意的k∈R,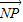 •
• =0恒成立,联立直线l与椭圆方程,消掉y得x的方程,由韦达定理及向量的数量积运算可把
=0恒成立,联立直线l与椭圆方程,消掉y得x的方程,由韦达定理及向量的数量积运算可把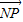 •
• =0化为关于k的恒等式,从而可得m的方程组,解出即可.
=0化为关于k的恒等式,从而可得m的方程组,解出即可.解答:解:(1)因为离心率为
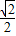 ,又2a=
,又2a=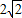 ,∴a=
,∴a=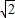 ,c=1,故b=1,故椭圆的方程为
,c=1,故b=1,故椭圆的方程为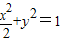 ;
;(2)设l的方程为y=kx-
 ,
,由
 得(2k2+1)x2-
得(2k2+1)x2- kx-
kx-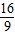 =0,
=0,设P(x1,y1),Q(x2,y2),则x1+x2=
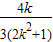 ,x1•x2=
,x1•x2=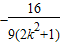 ,
,假设在y轴上存在定点N(0,m)满足题设,则
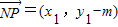 ,
,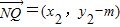 ,
,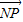 •
•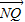 =x1x2+(y1-m)(y2-m)=x1x2+y1y2-m(y1+y2)+m2
=x1x2+(y1-m)(y2-m)=x1x2+y1y2-m(y1+y2)+m2=x1x2+(kx1-
 )( kx2-
)( kx2- )-m(kx1-
)-m(kx1- +kx2-
+kx2- )+m2
)+m2=(k2+1)x1x2-k(
 +m)•(x1+x2)+m2+
+m)•(x1+x2)+m2+ m+
m+
=
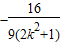 -k(
-k( +m)•
+m)• +m2+
+m2+ m+
m+
=
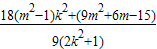 ,
,由假设得对于任意的k∈R,
 •
• =0恒成立,即
=0恒成立,即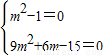 ,解得m=1,
,解得m=1,因此,在y轴上存在定点N,使得以PQ为直径的圆恒过这个点,点N的坐标为(0,1).
点评:本题考查直线与圆锥曲线的位置关系及椭圆方程的求解,考查向量的有关运算,考查学生分析解决问题的能力.

练习册系列答案
相关题目
 的中心是坐标原点,焦点在坐标轴上,且椭圆过点
的中心是坐标原点,焦点在坐标轴上,且椭圆过点 三点.
三点. 为椭圆
为椭圆 的任意一点,
的任意一点, ,求
,求 内切圆的面积的最大值,并指出其内切圆圆心的坐标.
内切圆的面积的最大值,并指出其内切圆圆心的坐标.