题目内容
曲线y=f(x)=ax3+bx2+cx,当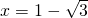 时,f(x)有极小值,当
时,f(x)有极小值,当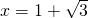 处有极大值,且在x=1处切线的斜率为
处有极大值,且在x=1处切线的斜率为 .
.
(I)求f(x);
(II)曲线上是否存在一点P,使得y=f(x)的图象关于点P中心对称?若存在,请求出点P坐标,并给出证明;若不存在,请说明理由.
解:(I)f′(x)=3ax2+2bx+c
∵当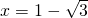 时,f(x)有极小值,当
时,f(x)有极小值,当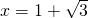 处有极大值
处有极大值
∴f′(1± )=0
)=0
即1± 为方程3ax2+2bx+c=0的两根
为方程3ax2+2bx+c=0的两根
∴-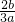 =(1+
=(1+ )+(1-
)+(1- )
)
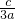 =(1+
=(1+ )(1-
)(1- )
)
∴b=-3a,c=-6a
又f(x)在x=1处切线的斜率为 .
.
∴f′(1)=
∴3a+2b+c=
∴a=- ,b=
,b= ,c=1
,c=1
∴f(x)=- x3+
x3+ x2+x
x2+x
(II)假设存在P(x0,y0)满足则f(x0+x)+f(x0-x)=2y0,
∴- (x0+x)3+
(x0+x)3+ (x0+x)2+(x0+x)-
(x0+x)2+(x0+x)- (x0-x)3+
(x0-x)3+ (x0-x)2+(x0-x)=2y0,
(x0-x)2+(x0-x)=2y0,
化简得(1-x0)x2+x02+2x0- x03=2y0,
x03=2y0,
∵上式任意x∈R等式成立
∴
∴x0=1,y0=
∴曲线上存在P(1, )满足题意
)满足题意
分析:(I)根据1± 是极值点可知f′(1±
是极值点可知f′(1± )=0,以及f′(1)=
)=0,以及f′(1)= 建立方程组,解之即可;
建立方程组,解之即可;
(II)假设存在P(x0,y0)满足则f(x0+x)+f(x0-x)=2y0,代入函数解析式,化简整理可求出所求.
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及函数在某点取得极值的条件,同时考查了方程组的解法,属于中档题.
∵当
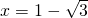 时,f(x)有极小值,当
时,f(x)有极小值,当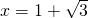 处有极大值
处有极大值∴f′(1±
 )=0
)=0即1±
 为方程3ax2+2bx+c=0的两根
为方程3ax2+2bx+c=0的两根∴-
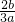 =(1+
=(1+ )+(1-
)+(1- )
)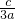 =(1+
=(1+ )(1-
)(1- )
)∴b=-3a,c=-6a
又f(x)在x=1处切线的斜率为
 .
.∴f′(1)=

∴3a+2b+c=

∴a=-
 ,b=
,b= ,c=1
,c=1∴f(x)=-
 x3+
x3+ x2+x
x2+x(II)假设存在P(x0,y0)满足则f(x0+x)+f(x0-x)=2y0,
∴-
 (x0+x)3+
(x0+x)3+ (x0+x)2+(x0+x)-
(x0+x)2+(x0+x)- (x0-x)3+
(x0-x)3+ (x0-x)2+(x0-x)=2y0,
(x0-x)2+(x0-x)=2y0,化简得(1-x0)x2+x02+2x0-
 x03=2y0,
x03=2y0,∵上式任意x∈R等式成立
∴

∴x0=1,y0=

∴曲线上存在P(1,
 )满足题意
)满足题意分析:(I)根据1±
 是极值点可知f′(1±
是极值点可知f′(1± )=0,以及f′(1)=
)=0,以及f′(1)= 建立方程组,解之即可;
建立方程组,解之即可;(II)假设存在P(x0,y0)满足则f(x0+x)+f(x0-x)=2y0,代入函数解析式,化简整理可求出所求.
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及函数在某点取得极值的条件,同时考查了方程组的解法,属于中档题.

练习册系列答案
相关题目