Question

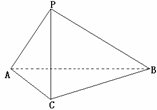 如图，三棱锥，

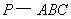（1）求证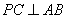：； （2）求二面角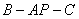的大小。

 

 

 

 

 

 

Answer 1

【答案】

 解法一：（1）取AB中点D，连接PD、CD

∵AP=BP                 ∴

∵AC=BC                 ∴

∵        ∴

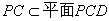∵          ∴（6分）

（2）∵AC=BC,AP=BP  ∴≌   又 ∴

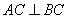又,即 且    ∴

取AP中点E，连结BE，CE     ∵     ∴

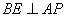
∵EC是BE在平面PAC内的射影         ∴

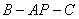∴是二面角的平面角（9分）

在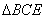中，

∴ （11分）

∴二面角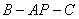的大小为（12分）

解法二：

（1）∵AC=BC，AP=BP ∴≌   又 ∴

∵ ∴   ∵ ∴（6分）

（2）如图，以C为原点建立空间直角坐标系

则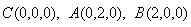设

∵ ∴

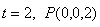
取AP中点E，连接BE,CE

∵                 ∴        

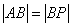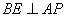
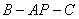∴是二面角的平面角（9分）

∵

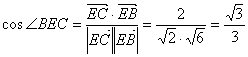∴（11分）

∴二面角的大小为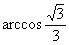(也可求法向量来求二面角的大小)（12分）