题目内容
已知在△ABC中,三条边a、b、c所对的角分别为A、B、C,向量 =(sinA,cosA),
=(sinA,cosA), =(cosB,sinB),且满足
=(cosB,sinB),且满足 .
.(1)求角C的大小;
(2)若sinA、sinC、sinB成等差数列,且
 =18,求c的值.
=18,求c的值.
【答案】分析:(1)直接将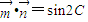 坐标化,化简整理即可求出C;
坐标化,化简整理即可求出C;
(2)由sinA,sinC,sinB成等差数列及正弦定理得a+b=2c,再由余弦定理得ab=c2,
由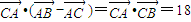 可得ab的关系,解方程组可求的c.
可得ab的关系,解方程组可求的c.
解答:解:(1)由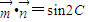 得sinAcosB+sinBcosA=sin(A+B)=sin2C,即sinC=sin2C,所以
得sinAcosB+sinBcosA=sin(A+B)=sin2C,即sinC=sin2C,所以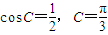 .
.
(2)∵sinA,sinC,sinB成等差数列,a+b=2c,
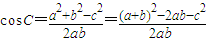 =
=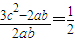 ∴ab=c2,
∴ab=c2,
由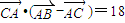 得
得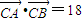 ,
,
即abcosC=18,所以ab=36,因此有c2=36,c=6.
点评:本题考查向量的运算、正余弦定理解三角形知识,考查利用所学知识分析问题、解决问题的能力.
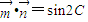 坐标化,化简整理即可求出C;
坐标化,化简整理即可求出C;(2)由sinA,sinC,sinB成等差数列及正弦定理得a+b=2c,再由余弦定理得ab=c2,
由
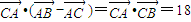 可得ab的关系,解方程组可求的c.
可得ab的关系,解方程组可求的c.解答:解:(1)由
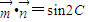 得sinAcosB+sinBcosA=sin(A+B)=sin2C,即sinC=sin2C,所以
得sinAcosB+sinBcosA=sin(A+B)=sin2C,即sinC=sin2C,所以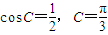 .
.(2)∵sinA,sinC,sinB成等差数列,a+b=2c,
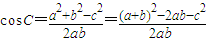 =
=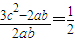 ∴ab=c2,
∴ab=c2,由
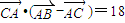 得
得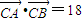 ,
,即abcosC=18,所以ab=36,因此有c2=36,c=6.
点评:本题考查向量的运算、正余弦定理解三角形知识,考查利用所学知识分析问题、解决问题的能力.

练习册系列答案
相关题目
 =(sinA,cosA),
=(sinA,cosA), =(cosB,sinB),且满足
=(cosB,sinB),且满足 .
. =18,求c的值.
=18,求c的值.