题目内容
10．已知函数g（x）=alnx-x+1，a∈R，求函数g（x）的单调区间．分析 确定函数的定义域，利用导数的正负，可得函数g（x）的单调区间．
解答 解：∵g（x）=alnx-x+1，定义域为（0，+∞），
∴g′（x）=$\frac{a-x}{x}$，
∴a≤0，g′（x）=$\frac{a-x}{x}$＜0，函数的单调减区间为（0，+∞）；
a＞0，g′（x）=$\frac{a-x}{x}$＜0，可得x＞a，g′（x）=$\frac{a-x}{x}$＞0，可得0＜x＜a，
∴函数的单调减区间为（a，+∞）；函数的单调增区间为（0，a）．
点评 本题考查了利用导数研究函数的单调性，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
20．
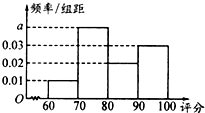为检测某种零件的生产质量，检验人员需抽取同批次的零件样本进行检测并评分．若检测后评分结果大于60分的零件为合格零件，评分结果不超过40分的零件将直接被淘汰，评分结果在（40，60]内的零件可能被修复也可能被淘汰．
（I）已知200个合格零件的评分结果的频率分布直方图如图所示．请根据此频率分布直方图，估计这200个零件评分结果的平均数和中位数；
（Ⅱ）根据已有的经验，可能被修复的零件个体被修复的概率如表：
假设每个零件被修复与否相互独立．现有5个零件的评分结果
为（单位：分）：38，43，45，52，58，记这5个零件被修复的个数为随机变量X，求X的分布列和数学期望．
为检测某种零件的生产质量，检验人员需抽取同批次的零件样本进行检测并评分．若检测后评分结果大于60分的零件为合格零件，评分结果不超过40分的零件将直接被淘汰，评分结果在（40，60]内的零件可能被修复也可能被淘汰．（I）已知200个合格零件的评分结果的频率分布直方图如图所示．请根据此频率分布直方图，估计这200个零件评分结果的平均数和中位数；
（Ⅱ）根据已有的经验，可能被修复的零件个体被修复的概率如表：
| 零件评分结果所在区间 | （40，50] | （50，60] |
| 每个零件个数被修复的概率 | $\frac{1}{3}$ | $\frac{1}{2}$ |
为（单位：分）：38，43，45，52，58，记这5个零件被修复的个数为随机变量X，求X的分布列和数学期望．
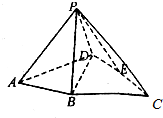已知四边形ABCD，AD=AB=BD=2，BC⊥BD，BC=$\sqrt{2}$BD，E为CD中点．现将△ABD沿BD折起，使点A到达点P，且AP=$\sqrt{6}$．
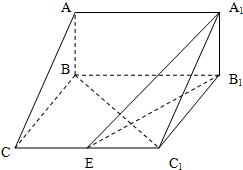如图，在三棱柱ABC-A1B1C1中，AB⊥侧面BB1C1C，已知AA1=2，AB=$\sqrt{2}$，BC=1，∠BCC1=$\frac{π}{3}$．