题目内容
【题目】已知圆M的圆心M在x轴上，半径为
，直线
被圆M截得的弦长为
，且圆心M在直线l的上方.
（1）求圆
的方程；
（2）设
，
，若圆M是
的内切圆，求AC，BC边所在直线的斜率（用t表示）；
（3）在（2）的条件下求的面积S的最大值及对应的t值.
【答案】（1）
（2）
；
（3）
的面积
的最大值为
，此时
或
【解析】
（1）设圆心
，求出点
到
的距离为1，解方程
即得解；
（2）设
斜率为
，
斜率为
，再根据直线和圆相切得到方程，解方程即得解；
（3）求出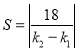
，再把
代入，结合
的范围求出面积的最大值和此时的值.
（1）设圆心，由已知得到的距离为
,
.
又
在
的上方，
，
，
，
故圆的方程为.
（2）设斜率为，斜率为，
则直线的方程为
，
直线的方程为
.
由于圆与相切，所以
，
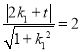；同理，
.
（3）联立两条直线方程得C点的横坐标为
，
由（2）得：，
，
，
，
，此时
，或.
综上：的面积的最大值为，此时或.
仁爱英语同步练习册系列答案
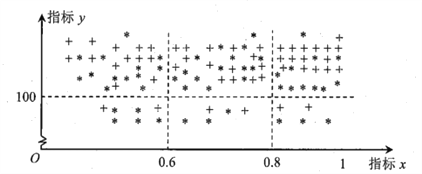
学习实践园地系列答案【题目】滕州市教育局为了解学生网络教学期间的学习情况，从初中及高中共抽取了50名学生，对他们每天平均学习时间进行统计．请根据下面的各班人数统计表和学习时间的频率分布直方图解决下列问题：
年级 | 人数 |
初一 | 4 |
初二 | 4 |
初三 | 6 |
高一 | 12 |
高二 | 6 |
高三 | 18 |
合计 | 50 |
（1）抽查的50人中，每天平均学习时间为6～8小时的人数有多少？
（2）经调查，每天平均学习时间不少于6小时的学生均来自高中．现采用分层抽样的方法，从学习时间不少于6小时的学生中随机抽取6名学生进行问卷调查，求这三个年级各抽取了多少名学生；
（3）在（2）抽取的6名学生中随机选取2人进行访谈，求这2名学生来自不同年级的概率．
【题目】对某城市居民家庭年收入
（万元）和年“享受资料消费”
（万元）进行统计分析，得数据如表所示.
| 6 | 8 | 10 | 12 |
| 2 | 3 | 5 | 6 |
（1）请根据表中提供的数据，用最小二乘法求出关于的线性回归方程
.
（2）若某家庭年收入为18万元，预测该家庭年“享受资料消费”为多少？
（参考公式：
，
）
【题目】某校高二奥赛班N名学生的物理测评成绩（满分120分）分布直方图如下，已知分数在100～110的学生数有21人。
（Ⅰ）求总人数N和分数在110～115分的人数n;
（Ⅱ）现准备从分数在110～115分的n名学生（女生占
）中任选2人，求其中恰好含有一名女生的概率；
（Ⅲ）为了分析某个学生的学习状态，对其下一阶段的学习提供指导性建议，对他前7次考试的数学成绩x（满分150分），物理成绩y进行分析，下面是该生7次考试的成绩。
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩y与数学成绩x是线性相关的，若该生的数学成绩达到130分，请你估计他的物理成绩大约是多少？
附：对于一组数据
其回归线
的斜率和截距的最小二乘估计分别为
．
