题目内容
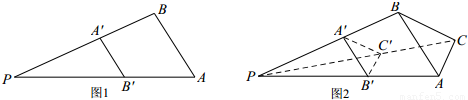
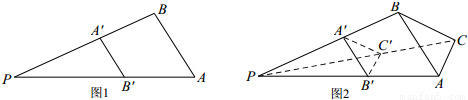
由图（1）有面积关系：
=
，则由（2）有体积关系：
=
=
| S△PA′B′ |
| S△PAB |
| PA′•PB′ |
| PA•PB |
| VP-A′B′C′ |
| VP-ABC |
| PA′•PB′•PC′ |
| PA•PB•PC |
| VP-A′B′C′ |
| VP-ABC |
| PA′•PB′•PC′ |
| PA•PB•PC |
分析：这是一个类比推理的题，在由平面图形到空间图形的类比推理中，一般是由点的性质类比推理到线的性质，由线的性质类比推理到面的性质，由面积的性质类比推理到体积性质．
解答：解：∵在由平面图形到空间图形的类比推理中，
一般是由点的性质类比推理到线的性质，
由线的性质类比推理到面的性质，
由面积的性质类比推理到体积性质．
故由
=
（面积的性质）
结合图（2）可类比推理出：
体积关系：
=
故答案为：
=
一般是由点的性质类比推理到线的性质，
由线的性质类比推理到面的性质，
由面积的性质类比推理到体积性质．
故由
| S△PA′B′ |
| S△PAB |
| PA′•PB′ |
| PA•PB |
结合图（2）可类比推理出：
体积关系：
| VP-A′B′C′ |
| VP-ABC |
| PA′•PB′•PC′ |
| PA•PB•PC |
故答案为：
| VP-A′B′C′ |
| VP-ABC |
| PA′•PB′•PC′ |
| PA•PB•PC |
点评：本小题主要考查类比推理．类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．
练习册系列答案
名校课堂系列答案
相关题目
，则由图（2）有体积关系：
= ．
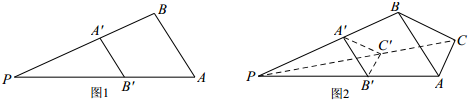
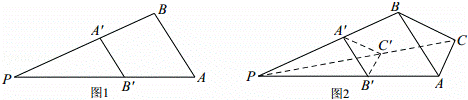
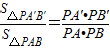，则由图（2）有体积关系：
= ．
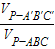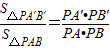，则由图（2）有体积关系：
= ．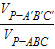