题目内容
(14分)已知函数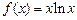 .
.
(1)求这个函数的图象在点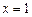 处的切线方程;
处的切线方程;
(2)讨论这个函数的单调区间.
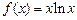 .
.(1)求这个函数的图象在点
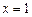 处的切线方程;
处的切线方程;(2)讨论这个函数的单调区间.
(1)
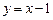
(2)
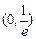
解: . (3分)
. (3分)
(1)当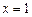 时,
时,
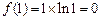 ,
,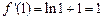 . (5分)
. (5分)
所以,切线过点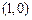 ,斜率为1, (7分)
,斜率为1, (7分)
故切线的方程为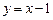 . (8分)
. (8分)
(2)令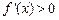 ,即
,即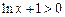 ,解得
,解得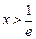 .
.
所以,函数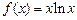 的单调递增区间为
的单调递增区间为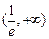 . (11分)
. (11分)
令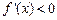 ,即
,即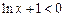 ,解得
,解得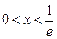 .
.
所以,函数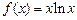 的单调递减区间为
的单调递减区间为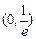 . (14分)
. (14分)
 . (3分)
. (3分)(1)当
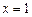 时,
时,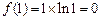 ,
,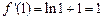 . (5分)
. (5分)所以,切线过点
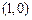 ,斜率为1, (7分)
,斜率为1, (7分)故切线的方程为
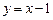 . (8分)
. (8分)(2)令
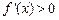 ,即
,即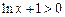 ,解得
,解得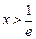 .
.所以,函数
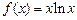 的单调递增区间为
的单调递增区间为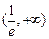 . (11分)
. (11分)令
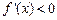 ,即
,即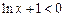 ,解得
,解得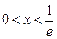 .
.所以,函数
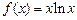 的单调递减区间为
的单调递减区间为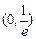 . (14分)
. (14分)
练习册系列答案
相关题目
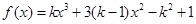 在区间(0,4)上是减函数,则k的取值范围( )
在区间(0,4)上是减函数,则k的取值范围( )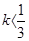
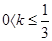
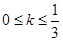
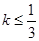
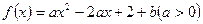 在区间
在区间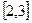 上的值域为
上的值域为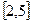
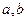
 的值
的值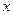 的函数
的函数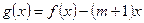 在
在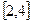 上为单调函数,求
上为单调函数,求 的取值范围
的取值范围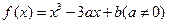 .
.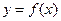 在点
在点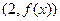
 处与直线
处与直线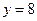 相切,求
相切,求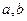 的值;
的值;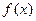 的单调区
的单调区 间与极值点.
间与极值点.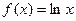 ,当
,当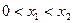 下列结论正确的是( )
下列结论正确的是( )
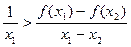
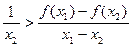
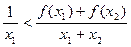
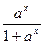 (a>0,且a≠1),〔m〕表示不超过实数m的最大整数,则
(a>0,且a≠1),〔m〕表示不超过实数m的最大整数,则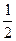 〕+〔f(-x)-
〕+〔f(-x)-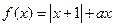 (
(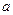 ∈R). 若函数f(x)在R上具有单调性,则
∈R). 若函数f(x)在R上具有单调性,则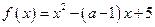 在区间
在区间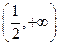 上为增函数,那么
上为增函数,那么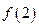 的取值范围是.
的取值范围是.