题目内容
已知圆![]() ,直线
,直线![]() .
.
(1)证明:不论![]() 为何值时,直线和圆恒相交于两点;
为何值时,直线和圆恒相交于两点;
(2)求直线![]() 被圆
被圆![]() 截得的弦长最小时的方程.
截得的弦长最小时的方程.
(2)![]()
解析:
(1)由![]() ,得
,得![]() .
.
解方程组![]() ,得
,得![]() ,
,
∴直线![]() 恒过定点
恒过定点![]() . .…….3分
. .…….3分
因为![]() ,
,
即![]() 到圆心
到圆心![]() 的距离
的距离![]() ,
,
∴A(3,1)在圆![]() 的内部,故
的内部,故![]() 与
与![]() 恒有两个公共点,
恒有两个公共点,
即不论![]() 为何值时,直线和圆恒相交于两点。 . .…….4分
为何值时,直线和圆恒相交于两点。 . .…….4分
(2)当直线![]() 被圆
被圆![]() 截得的弦长最小时,有
截得的弦长最小时,有![]() ,由
,由![]() ,
,
得![]() 的方程为
的方程为![]() ,即
,即![]() .. .……8分
.. .……8分

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
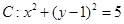 ,直线
,直线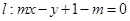 .
.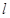 与圆C的位置关系;
与圆C的位置关系;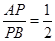 ,求此时直线
,求此时直线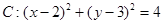 ,直线
,直线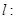
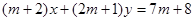 ,
,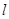 与圆
与圆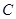 恒相交;
恒相交;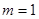 时,过圆
时,过圆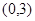 作圆的切线
作圆的切线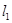 交直线
交直线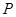 点,
点,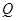 为圆
为圆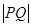 的取值范围;
的取值范围;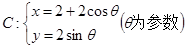 ,直线l:
,直线l: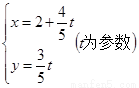
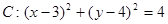 和直线
和直线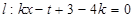 ,
,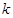 取什么值,直线和圆总相交;
取什么值,直线和圆总相交;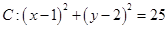 ,直线
,直线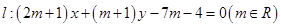 。
。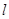 恒过定点,并求出该定点;
恒过定点,并求出该定点;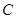 截得弦长最小时,求此时直线
截得弦长最小时,求此时直线