题目内容
已知圆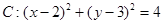 ,直线
,直线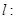
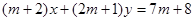 ,
,
(1)求证:直线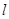 与圆
与圆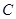 恒相交;
恒相交;
(2)当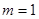 时,过圆
时,过圆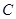 上点
上点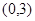 作圆的切线
作圆的切线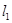 交直线
交直线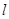 于
于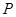 点,
点,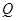 为圆
为圆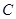 上的动点,求
上的动点,求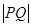 的取值范围;
的取值范围;
【答案】
(1)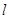 恒过两直线
恒过两直线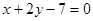 及
及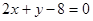 的交点
的交点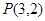 ;(2)
;(2) 。
。
【解析】
试题分析:(1)证明:由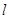 得方程得
得方程得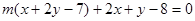 ,
,
故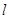 恒过两直线
恒过两直线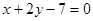 及
及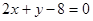 的交点
的交点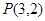 ,
,
 ,即点
,即点 在圆
在圆 内部,
内部,
 直线
直线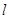 与圆
与圆 恒相交。
恒相交。
(2)由题知
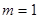 时,
时,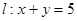
所以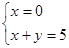

 ,而
,而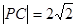 ,所以
,所以
考点:直线系方程;直线与圆的位置关系。
点评:定点直线系:若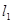 :
: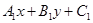 =0和
=0和 :
: =0相交,则过
=0相交,则过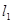 与
与 交点的直线系为
交点的直线系为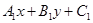 +λ
+λ =0。
=0。

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
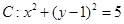 ,直线
,直线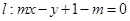 .
.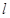 与圆C的位置关系;
与圆C的位置关系;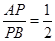 ,求此时直线
,求此时直线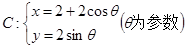 ,直线l:
,直线l: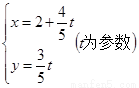
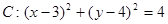 和直线
和直线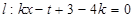 ,
,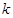 取什么值,直线和圆总相交;
取什么值,直线和圆总相交;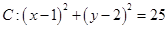 ,直线
,直线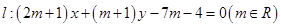 。
。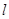 恒过定点,并求出该定点;
恒过定点,并求出该定点;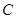 截得弦长最小时,求此时直线
截得弦长最小时,求此时直线