题目内容
(本题满分12分)
已知数列 的前
的前 项和为
项和为 ,
, (
( ).
).
(Ⅰ)证明数列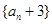 是等比数列,求出数列
是等比数列,求出数列 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和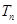 ;
;
(Ⅲ)数列 中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
(Ⅰ)见解析,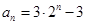 .
.
(Ⅱ) .
.
(Ⅲ)不存在满足条件的三项.
解析

练习册系列答案
相关题目
已知数列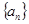 是等比数列,且
是等比数列,且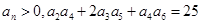 ,那么
,那么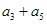 =( ).
=( ).
| A.5 | B.10 | C.15 | D.20 |
题目内容
(本题满分12分)
已知数列 的前
的前 项和为
项和为 ,
, (
( ).
).
(Ⅰ)证明数列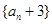 是等比数列,求出数列
是等比数列,求出数列 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和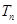 ;
;
(Ⅲ)数列 中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
(Ⅰ)见解析,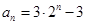 .
.
(Ⅱ) .
.
(Ⅲ)不存在满足条件的三项.
解析

已知数列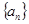 是等比数列,且
是等比数列,且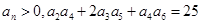 ,那么
,那么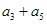 =( ).
=( ).
| A.5 | B.10 | C.15 | D.20 |