题目内容
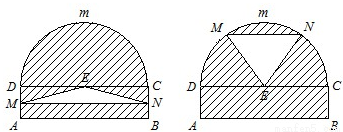
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.(1)设MN与AB之间的距离为x米,试将△EMN的面积S(平方米)表示成关于x的函数;
(2)求△EMN的面积S(平方米)的最大值.

【答案】分析:(1)分类求出MN在矩形区域、三角形区域滑动时,△EMN的面积,可得分段函数;
(2)分类求出△EMN的面积的最值,比较其大小,即可得到最值.
解答: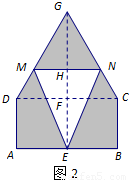
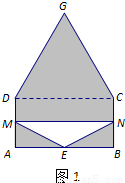 解:(1)①如图1所示,当MN在矩形区域滑动,即0<x≤1时,△EMN的面积S=
解:(1)①如图1所示,当MN在矩形区域滑动,即0<x≤1时,△EMN的面积S=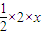 =x;(1分)
=x;(1分)
②如图2所示,当MN在三角形区域滑动,即1<x<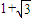 时,连接EG,交CD于点F,交MN于点H,
时,连接EG,交CD于点F,交MN于点H,
∵E为AB中点,
∴F为CD中点,GF⊥CD,且FG= .
.
又∵MN∥CD,∴△MNG∽△DCG.
∴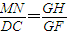 ,即
,即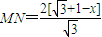 .(4分)
.(4分)
故△EMN的面积S=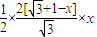 =
=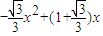 ; (6分)
; (6分)
综合可得: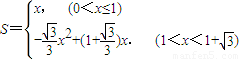 (7分)
(7分)
(2)①当MN在矩形区域滑动时,S=x,所以有0<S≤1;(8分)
②当MN在三角形区域滑动时,S=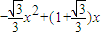 .
.
因而,当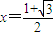 (米)时,S得到最大值,最大值S=
(米)时,S得到最大值,最大值S=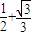 (平方米).
(平方米).
∵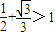 ,
,
∴S有最大值,最大值为 平方米.(12分)
平方米.(12分)
点评:本题考查函数模型的建立,考查函数的最值,考查学生分析解决问题的能力,确定分段函数是关键.
(2)分类求出△EMN的面积的最值,比较其大小,即可得到最值.
解答:

 解:(1)①如图1所示,当MN在矩形区域滑动,即0<x≤1时,△EMN的面积S=
解:(1)①如图1所示,当MN在矩形区域滑动,即0<x≤1时,△EMN的面积S=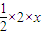 =x;(1分)
=x;(1分)②如图2所示,当MN在三角形区域滑动,即1<x<
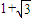 时,连接EG,交CD于点F,交MN于点H,
时,连接EG,交CD于点F,交MN于点H,∵E为AB中点,
∴F为CD中点,GF⊥CD,且FG=
 .
.又∵MN∥CD,∴△MNG∽△DCG.
∴
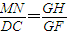 ,即
,即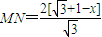 .(4分)
.(4分)故△EMN的面积S=
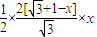 =
=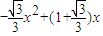 ; (6分)
; (6分)综合可得:
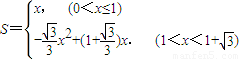 (7分)
(7分)(2)①当MN在矩形区域滑动时,S=x,所以有0<S≤1;(8分)
②当MN在三角形区域滑动时,S=
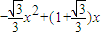 .
.因而,当
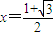 (米)时,S得到最大值,最大值S=
(米)时,S得到最大值,最大值S=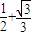 (平方米).
(平方米).∵
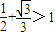 ,
,∴S有最大值,最大值为
 平方米.(12分)
平方米.(12分)点评:本题考查函数模型的建立,考查函数的最值,考查学生分析解决问题的能力,确定分段函数是关键.

练习册系列答案
相关题目
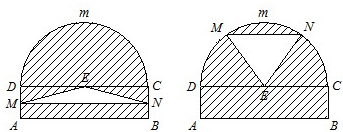 (2009•普陀区二模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆(MN和AB、DC不重合).
(2009•普陀区二模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆(MN和AB、DC不重合).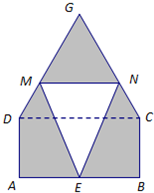 (2013•静安区一模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
(2013•静安区一模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.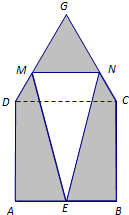 (2013•静安区一模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是正方形,其中AB=2米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
(2013•静安区一模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是正方形,其中AB=2米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.