题目内容
2．已知等比数列{an}的前3项的和是-$\frac{3}{5}$，前6项的和是$\frac{21}{5}$，求它的前10项的和．分析 设等比数列{an}的公比为q，由题意可得a1+a2+a3=$-\frac{3}{5}$，a1+a2+a3+a4+a5+a6=$\frac{21}{5}$，两式联立解得a1和q由求和公式可得．
解答 解：设等比数列{an}的公比为q，
由题意可得a1+a2+a3=$-\frac{3}{5}$，a1+a2+a3+a4+a5+a6=$\frac{21}{5}$，
两式相减可得a4+a5+a6=$\frac{21}{5}$-（$-\frac{3}{5}$）=$\frac{24}{5}$，
∴q3=$\frac{{a}_{4}+{a}_{5}+{a}_{6}}{{a}_{1}+{a}_{2}+{a}_{3}}$=-8，解得q=-2，
代入a1+a2+a3=$-\frac{3}{5}$可得a1（1-2+4）=$-\frac{3}{5}$，解得a1=$-\frac{1}{5}$，
∴前10项的和S10=$\frac{-\frac{1}{5}[1-（-2）^{10}]}{1-（-2）}$=$\frac{3069}{5}$
点评 本题考查等比数列的求和公式，求出数列的首项和公比是解决问题的关键，属基础题．
练习册系列答案
相关题目
13．若圆x2+y2-4kx-2y+4k2=0的一条直径所在直线方程为x-2y-2=0，则实数k的值为（ ）
| A． | 2 | B． | 4 | C． | -$\frac{1}{4}$ | D． | -$\frac{1}{2}$ |
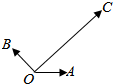如图，已知|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1，$\overrightarrow{OA}与\overrightarrow{OB}$的夹角为120°，$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°，|$\overrightarrow{OC}$|=2$\sqrt{3}$，用$\overrightarrow{OA}、\overrightarrow{OB}$表示$\overrightarrow{OC}$．
11．表示两直线x-2y+3=0与3x+2y+1=0交点的集合，正确的是 （ ）
| A． | {-1，1} | B． | {（-1，1）} | C． | {（1，-1）} | D． | {1，-1} |