题目内容
20.函数f(x)=lnx+ln(2-x)+x的单调递增区间是(0,$\sqrt{2}$].分析 由函数的解析式求得函数的定义域,令导数大于或等于零,求得x的范围,再结合定义域求得函数的增区间.
解答 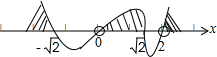 解:∵函数f(x)=lnx+ln(2-x)+x,∴$\left\{\begin{array}{l}{x>0}\\{2-x>0}\end{array}\right.$,
解:∵函数f(x)=lnx+ln(2-x)+x,∴$\left\{\begin{array}{l}{x>0}\\{2-x>0}\end{array}\right.$,
求得0<x<2,故函数的定义域为(0,2),
由f′(x)=$\frac{1}{x}$-$\frac{1}{2-x}$+1=$\frac{{x}^{2}-2}{x(x-2)}$≥0,
用穿根法求得0<x≤$\sqrt{2}$,或x<-$\sqrt{2}$,或 x>2,
结合函数的定义域可得函数的增区间为 $(0,\sqrt{2}]$,
故答案为:$(0,\sqrt{2}]$.
点评 本题主要考查求函数的定义域,利用导数研究函数的单调性,用穿根法解分式不等式,属于中档题.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
8.抛物线y2=8x的焦点坐标是( )
| A. | (4,0) | B. | (2,0) | C. | (0,2) | D. | (0,4) |
15.过抛物线y2=4x的焦点F的直线l交抛物线于A,B两点.若AB中点M到抛物线准线的距离为6,则线段AB的长为( )
| A. | 6 | B. | 9 | C. | 12 | D. | 无法确定 |
5.x=-$\frac{1}{4}$为准线的抛物线的标准方程为( )
| A. | y2=x | B. | y2=$\frac{1}{2}$x | C. | x2=$\frac{1}{2}$y | D. | x2=y |
9.抛物线y2=-4x的准线方程为( )
| A. | x=-1 | B. | x=1 | C. | x=2 | D. | x=-2 |
 已知抛物线E:x2=2py (p>0)上一点T(t,4)( t>0)到其焦点F的距离为5,经过点Q(1,1)作斜率为k(k∈R)的直线交抛物线E于A、B两点,抛物线E分别在点A、B处的切线相交于点P.
已知抛物线E:x2=2py (p>0)上一点T(t,4)( t>0)到其焦点F的距离为5,经过点Q(1,1)作斜率为k(k∈R)的直线交抛物线E于A、B两点,抛物线E分别在点A、B处的切线相交于点P.