题目内容
椭圆 的焦点为
的焦点为 ,点
,点 在椭圆上,若
在椭圆上,若 ,
, 的大小为 .
的大小为 .
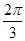
解析试题分析:由椭圆方程知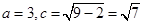 ,由椭圆的定义可得
,由椭圆的定义可得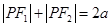 ,所以
,所以 ,又因为
,又因为 ,所以在
,所以在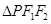 中
中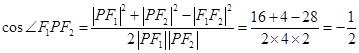 ,因为
,因为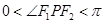 ,所以
,所以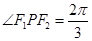 。
。
考点:1椭圆的定义;2余弦定理。

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
题目内容
椭圆 的焦点为
的焦点为 ,点
,点 在椭圆上,若
在椭圆上,若 ,
, 的大小为 .
的大小为 .
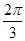
解析试题分析:由椭圆方程知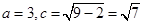 ,由椭圆的定义可得
,由椭圆的定义可得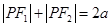 ,所以
,所以 ,又因为
,又因为 ,所以在
,所以在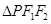 中
中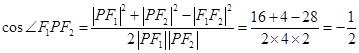 ,因为
,因为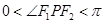 ,所以
,所以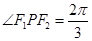 。
。
考点:1椭圆的定义;2余弦定理。

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案