题目内容
甲乙二人轮流掷一枚均匀的正方体骰子,规定:如果某人某一次掷出1点,则下一次继续由此人掷,如果掷出其他点数,则由另一人来掷,且第一次由甲掷.设第n次由甲掷的概率为pn,由乙掷的概率为qn.
(1)计算p2,p3的值;
(2)求证{pn-qn}是等比数列;
(3)求pn.
(1)计算p2,p3的值;
(2)求证{pn-qn}是等比数列;
(3)求pn.
(1)p2=,p3=p2+q2=;(2)同解析;(3)pn=。
(1)由已知,p1=1,q1=0 ---1分 p2=,且q2=
p3=p2+q2=
(2)由已知,pn=pn-1+qn-1,qn=qn-1+pn-1(n≥2)
两式相减得:pn-qn=(pn-1-qn-1)+(qn-1-pn-1) =-(pn-1-qn-1)
即数列{pn-qn}是公比为-等比数列;
(3)由(2)得:pn-qn=(-)n-1(p1-q1)=(-)n-1
又pn+qn=1 ∴pn=(-)n-1+qn=(-)n-1+(1-pn)
∴pn=(-)n-1+(n∈N+) ∴pn=.
p3=p2+q2=
(2)由已知,pn=pn-1+qn-1,qn=qn-1+pn-1(n≥2)
两式相减得:pn-qn=(pn-1-qn-1)+(qn-1-pn-1) =-(pn-1-qn-1)
即数列{pn-qn}是公比为-等比数列;
(3)由(2)得:pn-qn=(-)n-1(p1-q1)=(-)n-1
又pn+qn=1 ∴pn=(-)n-1+qn=(-)n-1+(1-pn)
∴pn=(-)n-1+(n∈N+) ∴pn=.

练习册系列答案
相关题目
 ,家用天然气的二氧化碳排放量(千克)=天然气使用立方数
,家用天然气的二氧化碳排放量(千克)=天然气使用立方数 等.某校开展“节能减排,保护环境,从我做起!”的活动,该校高一、六班同学利用假期在东城、西城两个小区进行了逐户的关于“生活习惯是否符合低碳排放标准”的调查.生活习惯符合低碳观念的称为“低碳家庭”,否则称为“非低碳家庭”.经统计,这两类家庭占各自小区总户数的比例
等.某校开展“节能减排,保护环境,从我做起!”的活动,该校高一、六班同学利用假期在东城、西城两个小区进行了逐户的关于“生活习惯是否符合低碳排放标准”的调查.生活习惯符合低碳观念的称为“低碳家庭”,否则称为“非低碳家庭”.经统计,这两类家庭占各自小区总户数的比例 数据如下:
数据如下:
 个家庭中恰好有两个家庭是“低碳家庭”的概率;
个家庭中恰好有两个家庭是“低碳家庭”的概率; 的家庭能加入到“低碳家庭”的行列中.宣传两周后随机地从东城小区中任选
的家庭能加入到“低碳家庭”的行列中.宣传两周后随机地从东城小区中任选 个家庭,记
个家庭,记 表示
表示 和
和 .
.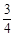 , B小区已经收到邀请的人选择参加“幸福愿景”座谈会的概率是
, B小区已经收到邀请的人选择参加“幸福愿景”座谈会的概率是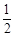 .
.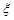 ,试求
,试求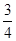 ,用满10000小时未坏的概率是
,用满10000小时未坏的概率是 ,现有一个此种元件,已经用过6000小时未坏,则它能用到10000小时的概率是 .
,现有一个此种元件,已经用过6000小时未坏,则它能用到10000小时的概率是 . ,刮风的概率是
,刮风的概率是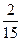 ,既刮风又下雨的概率为
,既刮风又下雨的概率为 ,设A为下雨,B为刮风,则
,设A为下雨,B为刮风,则 = ( )
= ( )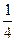 (B)
(B)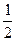 (C)
(C) (D)
(D)