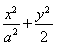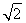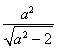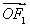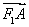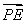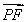题目内容
设数列{an}:1,-2,-2,3,3,3,-4,-4,-4,-4,…,(-1)k-1k,…,(-1)k-1k,…,即当 <n≤
<n≤ (k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*).对于l∈N*,定义集合Pl={n|Sn是an的整数倍,n∈N*,且1≤n≤l}.
(k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*).对于l∈N*,定义集合Pl={n|Sn是an的整数倍,n∈N*,且1≤n≤l}.
(1)求集合P11中元素的个数;
(2)求集合P2 000中元素的个数.
(1)5 (2) 1 008
【解析】
解 (1)由数列{an}的定义得a1=1,a2=-2,a3=-2,a4=3,a5=3,a6=3,a7=-4,a8=-4,a9=-4,a10=-4,a11=5,所以S1=1,S2=-1,S3=-3,S4=0,S5=3,S6=6,S7=2,S8=-2,S9=-6,S10=-10,S11=-5,从而S1=a1,S4=0×a4,S5=a5,S6=2a6,S11=-a11,所以集合P11中元素的个数为5.
(2)先证:Si(2i+1)=-i(2i+1)(i∈N*).
事实上,①当i=1时,Si(2i+1)=S3=-3,-i(2i+1)=-3,故原等式成立;
②假设i=m时成立,即Sm(2m+1)=-m(2m+1),则i=m+1时 ,S(m+1)(2m+3)=Sm(2m+1)+(2m+1)2-(2m+2)2=-m(2m+1)-4m-3=-(2m2+5m+3)=-(m+1)(2m+3).
综合①②可得Si(2i+1)=-i(2i+1).于是
S(i+1)(2i+1)=Si(2i+1)+(2i+1)2=-i(2i+1)+(2i+1)2=(2i+1)(i+1).
由上可知Si(2i+1)是2i+1的倍数,而ai(2i+1)+j=2i+1(j=1,2,…,2i+1),所以Si(2i+1)+j=Si(2i+1)+j(2i+1)是ai(2i+1)+j(j=1,2,…,2i+1)的倍数.又S(i+1)(2i+1)=(i+1)·(2i+1)不是2i+2的倍数,而a(i+1)(2i+1)+j=-(2i+2)(j=1,2,…,2i+2),所以S(i+1)(2i+1)+j=S(i+1)(2i+1)-j(2i+2)=(2i+1)(i+1)-j(2i+2)不是a(i+1)(2i+1)+j(j=1,2,…,2i+2)的倍数,故当l=i(2i+1)时,集合Pl中元素的个数为1+3+…+(2i-1)=i2,于是,当l=i(2i+1)+j(1≤j≤2i+1)时,集合Pl中元素的个数为i2+j.
又2 000=31×(2×31+1)+47,故集合P2 000中元素的个数为312+47=1 008.

 阅读快车系列答案
阅读快车系列答案抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结果如下:
运动员 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
甲 | 87 | 91 | 90 | 89 | 93 |
乙 | 89 | 90 | 91 | 88 | 92 |
则成绩较为稳定(方差较小)的那位运动员成绩的方差为________.