题目内容

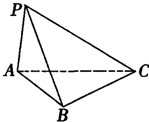三棱锥P-ABC中，底面△ABC是边长为2的正三角形，PA⊥底面ABC，且PA=2，则此三棱锥外接球的半径为（　　）
分析：由已知结合三棱锥和正三棱柱的几何特征，可得此三棱锥外接球，即为以△ABC为底面以PA为高的正三棱柱的外接球，分别求出棱锥底面半径r，和球心距d，代入R=
r2+d2
，可得球的半径R
解答：解：根据已知中底面△ABC是边长为2的正三角形，PA⊥底面ABC，
可得此三棱锥外接球，即为以△ABC为底面以PA为高的正三棱柱的外接球
∵△ABC是边长为2的正三角形，
∴△ABC的外接圆半径r=
2
3
3
，球心到△ABC的外接圆圆心的距离d=1
故球的半径R=
r2+d2
=
7
3
=
21
3

故选D
点评：本题考查的知识点是球内接多面体，熟练掌握球的半径R公式R=
r2+d2
，是解答的关键．
练习册系列答案
相关题目
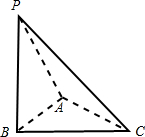精英家教网如图，在三棱锥P-ABC中，△PAB是等边三角形，∠PAC=∠PBC=90°．
（1）证明：AB⊥PC；
（2）若PC=4，且平面PAC⊥平面PBC，求三棱锥P-ABC的体积．
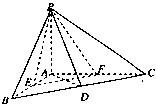精英家教网如图，在三棱锥P-ABC中，PA⊥平面ABC，∠BAC=
π2
，PA=2，AB=AC=4，点D、E、F分别为BC、AB、AC的中点．
（I）求证：EF⊥平面PAD；
（II）求点A到平面PEF的距离；
（III）求二面角E-PF-A的大小．
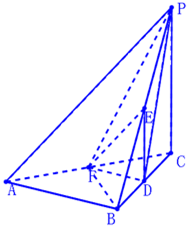精英家教网如图，在三棱锥P-ABC中，AB⊥BC，AB=BC=kPA，点O、D分别是AC、PC的中点，OP⊥底面ABC．
（Ⅰ）当k=
12
时，求直线PA与平面PBC所成角的大小；
（Ⅱ）当k取何值时，O在平面PBC内的射影恰好为△PBC的重心？
精英家教网如图，在三棱锥P-ABC中，PC⊥平面ABC，△ABC为正三角形，D、E、F分别是BC，PB，CA的中点．
（1）证明平面PBF⊥平面PAC；
（2）判断AE是否平行于平面PFD，并说明理由；
（3）若PC=AB=2，求三棱锥P-DEF的体积．
在正三棱锥P-ABC中，M，N分别是PB，PC的中点，若截面AMN⊥侧面PBC，则此棱锥截面与底面所成的二面角正弦值是
6
6
6
6
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网