题目内容
直线x-my+2=0与抛物线y=
x2有且只有一个公共点,则m=
| 1 |
| 4 |
0或-
| 1 |
| 2 |
0或-
.| 1 |
| 2 |
分析:联立方程组消x得关于y的方程,分m=0,m≠0两种情况讨论,使该方程有一解即可.
解答:解:由
得m2y2-(4m+4)y+4=0,
(1)当m=0时,-4y+4=0,解得y=1,此时交点为(-2,1),直线与抛物线只有一个公共点;
(2)当m≠0时,由△=(4m+4)2-16m2=0,得m=-
,此时直线与抛物线相切,只有一个公共点;
综上,m=0或-
.
故答案为:0或-
.
|
(1)当m=0时,-4y+4=0,解得y=1,此时交点为(-2,1),直线与抛物线只有一个公共点;
(2)当m≠0时,由△=(4m+4)2-16m2=0,得m=-
| 1 |
| 2 |
综上,m=0或-
| 1 |
| 2 |
故答案为:0或-
| 1 |
| 2 |
点评:本题考查直线与圆锥曲线的位置关系,常用方法为:(1)代数法:转化为方程组解的个数;(2)数形结合:利用圆锥曲线的性质;

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
如果直线x-my+2=0与圆x2+(y-1)2=1有两个不同的交点,则( )
A、m≥
| ||
B、m>
| ||
C、m<
| ||
D、m≤
|
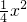 有且只有一个公共点,则m=________.
有且只有一个公共点,则m=________.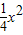 有且只有一个公共点,则m= .
有且只有一个公共点,则m= .