题目内容
已知由正数组成的两个数列{an},{bn},如果an,an+1是关于x的方程x2-2bn2x+anbnbn+1=0的两根.(1)求证:{bn}为等差数列;
(2)已知a1=2,a2=6,分别求数列{an},{bn}的通项公式;
(3)求数{
| bn | 2n |
分析:(1)根据题中已知条件和函数中根与系数的关系便可求出bn与bn-1、bn+1的关系,即可证明{bn}为等差数列;
(2)将a1=2,a2=6代入an+an+1=2bn2即可求出b1的值,进而求出{bn}的通项公式,然后将{bn}的通项公式代入an=bn-1bn即可求出数列{an}的通项公式;
(3)将数列{bn}的通项公式代入{
}中即可求出其表达式,然后求出其前n项和Sn的表达式,然后利用错位相减法求出
Sn的表达式,即可求出Sn的表达式.
(2)将a1=2,a2=6代入an+an+1=2bn2即可求出b1的值,进而求出{bn}的通项公式,然后将{bn}的通项公式代入an=bn-1bn即可求出数列{an}的通项公式;
(3)将数列{bn}的通项公式代入{
| bn |
| 2n |
| 1 |
| 2 |
解答:解:(1)由:an,an+1是关于x的方程x2-2bn2x+anbnbn+1=0的两根,
得:an+an+1=2bn2,anan+1=anbnbn+1…(2分)
∴2bn2=bn-1bn+bnbn+1,
∵bn>0,
∴2bn=bn-1+bn+1(n>1)
∴{bn}是等差数列 …(4分)
(2)由(1)知2b12=a1+a2=8,
∴b1=2,
∵a2=b1b2,
∴b2=3,
∴bn=n+1,
∴bn-1=n…(6分)
an=bn-1bn=n(n+1)(n>1)…(7分)
又a1=2符合上式,∴an=n(n+1)…(9分)
(3)Sn=
+
+
+…+
①
Sn=
+
+…+
②
①-②得
Sn=1+
+
+
+…+
-
…(13分)
=1+
-
=1+
(1-
)-
∴Sn=3-
…(16分)
得:an+an+1=2bn2,anan+1=anbnbn+1…(2分)
∴2bn2=bn-1bn+bnbn+1,
∵bn>0,
∴2bn=bn-1+bn+1(n>1)
∴{bn}是等差数列 …(4分)
(2)由(1)知2b12=a1+a2=8,
∴b1=2,
∵a2=b1b2,
∴b2=3,
∴bn=n+1,
∴bn-1=n…(6分)
an=bn-1bn=n(n+1)(n>1)…(7分)
又a1=2符合上式,∴an=n(n+1)…(9分)
(3)Sn=
| 2 |
| 2 |
| 3 |
| 22 |
| 4 |
| 23 |
| n+1 |
| 2n |
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n+1 |
| 2n+1 |
①-②得
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n |
| n+1 |
| 2n+1 |
=1+
| ||||
1-
|
| n-1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| n-1 |
| 2n+1 |
∴Sn=3-
| n+3 |
| 2n |
点评:本题以函数中根与系数的关系为立足点考查了数列的通项公式及前n项和的求法,考查了学生的计算能力和对数列与函数的综合掌握,是各地高考的热点,解题时注意整体思想和转化思想的运用,属于中档题.

练习册系列答案
相关题目
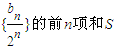 .
.