题目内容
解不等式:解关于x的不等式:
<x(其中a>0)
| (a+1)x2-2 | ax+1 |
分析:把不等式的右边移项到左边,合并后转化为x+1,x-2与x+
的积小于0,然后分三种情况考虑:a大于1,a=1和0<a<1三种情况分别求出相应的解集,最后综上,列举出各种情况的解集即为原不等式的解集.
| 1 |
| a |
解答:解:
<x?
-x<0?
<0?(x+1)(x-2)(x+
)<0
①当0<a<1时,原不等式的解集为 (-∞,-
)∪(-1,2)
②当a=1时,原不等式的解集为 (-∞,-1)∪(-1,2)
③当a>1时 原不等式的解集为 (-∞,-1)∪(-
,2)
| (a+1)x2-2 |
| ax+1 |
| (a+1)x2-2 |
| ax+1 |
| (x+1)(x-2) |
| ax+1 |
| 1 |
| a |
①当0<a<1时,原不等式的解集为 (-∞,-
| 1 |
| a |
②当a=1时,原不等式的解集为 (-∞,-1)∪(-1,2)
③当a>1时 原不等式的解集为 (-∞,-1)∪(-
| 1 |
| a |
点评:此题考查了其他不等式的解法,考查了分类讨论的数学思想,是一道中档题.

练习册系列答案
相关题目
 (其中a>0)
(其中a>0)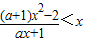 (其中a>0)
(其中a>0)