题目内容
3.定义在[1,+∞)上的函数f(x)满足f(x+2)=f(x)+x,且当x∈[0,2)时,f(x)=x,则f(101)=2501.分析 由f(x+2)=f(x)+x可得f(x+2)-f(x)=x,从而写出f(101)-f(99)=99,f(99)-f(97)=97,f(97)-f(95)=95,…f(3)-f(1)=1,再由叠加法求和即可.
解答 解:∵f(x+2)=f(x)+x,
∴f(x+2)-f(x)=x,
∴f(101)-f(99)=99,
f(99)-f(97)=97,
f(97)-f(95)=95,
…
f(3)-f(1)=1,
f(1)=1;
求和得,
f(101)=1+1+3+5+…+95+97+99=2501;
故答案为:2501.
点评 本题考查了函数的性质的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
18.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,收集数据如下:
(1)画出散点图;
(2)求回归方程;
(3)关于加工零件的个数与加工时间,你能得出什么结论?
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 加工时间y(min) | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(2)求回归方程;
(3)关于加工零件的个数与加工时间,你能得出什么结论?
11.已知直线l1:ax+2y+1=0,l2:(3-a)x-y+a=0,则条件“a=1”是“l1⊥l2“的( )
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不必要也不充分条件 |
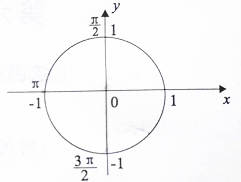 单位圆上三角函数值的集合解释是“角在弧上,值在线上”,试在图中画出α属于第Ⅲ象限的一个正弦值,余弦值.
单位圆上三角函数值的集合解释是“角在弧上,值在线上”,试在图中画出α属于第Ⅲ象限的一个正弦值,余弦值.