题目内容
已知定义域为 的函数
的函数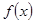 是奇函数,当
是奇函数,当 时,
时, |
| |
|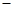
 ,且对
,且对 ,恒有
,恒有 ,则实数
,则实数 的取值范围为( )
的取值范围为( )
A.[0,2] B.[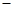
 ,
, ] C.[
] C.[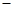 1,1] D.[
1,1] D.[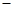 2,0]
2,0]
【答案】
B
【解析】
试题分析:由题意可知当 时,
时,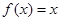 符号题目要求;
符号题目要求;
当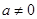 时,因为当
时,因为当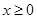 时,
时,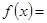 |
| |
|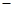
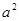 ,
,
所以当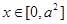 时,
时,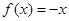 ,单调递减,当
,单调递减,当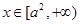 时,
时,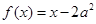 ,单调递增;
,单调递增;
因为函数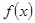 是奇函数,所以当
是奇函数,所以当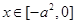 时,单调递减,当
时,单调递减,当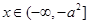 时,单调递增;
时,单调递增;
综上所述,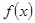 在
在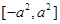 上递减,区间长度为
上递减,区间长度为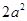 ,
,
又因为对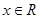 ,恒有
,恒有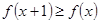 ,所以
,所以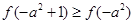 ,需要
,需要
考点:本小题主要考查含绝对值的函数的单调性、奇偶性的应用和函数恒成立问题,考查学生分析问题、解决问题的能力和运算求解能力.
点评:含绝对值的函数近几年高考中常常出现,关键是分类讨论去掉绝对值符号,而恒成立问题一般转化为求最值问题解决.

练习册系列答案
相关题目
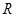 的函数
的函数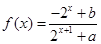 是奇函数。
是奇函数。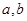 的值;
的值;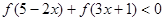
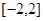 的函数
的函数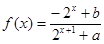 是奇函数.
是奇函数.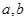 的值; (Ⅱ)解关于
的值; (Ⅱ)解关于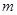 的不等式
的不等式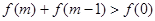 .
.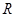 的函数
的函数 是奇函数.
是奇函数. 的值;
的值;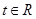 ,不等式
,不等式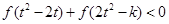 恒成立,求
恒成立,求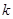 的取值范围.
的取值范围.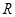 的函数
的函数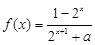 是奇函数.
是奇函数.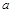 的值;
的值;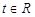 ,不等式
,不等式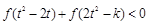 恒成立,求实数
恒成立,求实数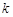 的取值范围.
的取值范围. 的函数
的函数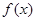 是偶函数,当
是偶函数,当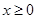 时,
时,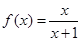 .
.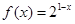 在区间
在区间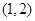 上有解
上有解