题目内容
1.化简:(1)$\frac{\sqrt{a}}{a-\sqrt{ab}}+\frac{\sqrt{a}}{a+\sqrt{ab}}$
(2)$\frac{1-\frac{1}{1+a}}{1+\frac{1}{a-1}}$
(3)$\frac{2+\frac{1}{x-1}-\frac{1}{x+1}}{x+\frac{x}{x^2-1}}$.
分析 直接利用根式以及有理指数幂的运算法则求解即可.
解答 解:(1)$\frac{\sqrt{a}}{a-\sqrt{ab}}+\frac{\sqrt{a}}{a+\sqrt{ab}}$
=$\frac{1}{\sqrt{a}-\sqrt{b}}+\frac{1}{\sqrt{a}+\sqrt{b}}$
=$\frac{\sqrt{a}+\sqrt{b}+\sqrt{a}-\sqrt{b}}{(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})}$
=$\frac{2\sqrt{a}}{a-b}$.
(2)$\frac{1-\frac{1}{1+a}}{1+\frac{1}{a-1}}$
=$\frac{\frac{1+a-1}{1+a}}{\frac{a-1+1}{a-1}}$
=$\frac{a-1}{1+a}$.
(3)$\frac{2+\frac{1}{x-1}-\frac{1}{x+1}}{x+\frac{x}{x^2-1}}$
=$\frac{\frac{2(x-1)(x+1)+x+1-x+1}{(x-1)(x+1)}}{\frac{{x}^{3}-x+x}{{x}^{2}-1}}$
=$\frac{2{x}^{2}}{{x}^{3}}$
=$\frac{2}{x}$.
点评 本题考查根式以及有理指数幂的化简求解,是基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
6.若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$+$\overrightarrow{b}$=(-2,-1),$\overrightarrow{a}$-$\overrightarrow{b}$=(4,-3),则$\overrightarrow{a}$•$\overrightarrow{b}$等于( )
| A. | -5 | B. | -1 | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
13.已知点P(x,y)满足$\left\{\begin{array}{l}{x≥1}\\{y≤1}\\{x-y-1≤0}\end{array}\right.$,目标函数z=x+ay(a<0)的最大值与最小值之和为0,则a的值为( )
| A. | -$\frac{3}{2}$ | B. | -2 | C. | -1 | D. | -$\frac{1}{2}$ |
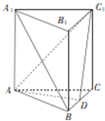 如图,在三棱柱ABC-A1B1C1中,底面ABC为正三角形,CC1⊥平面ABC,AB=AA1,D是BC上的一点,且AD⊥C1D.
如图,在三棱柱ABC-A1B1C1中,底面ABC为正三角形,CC1⊥平面ABC,AB=AA1,D是BC上的一点,且AD⊥C1D.