题目内容
6.已知函数f(x)=$\frac{{x}^{2}}{ax+b}$(a,b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.(1)求函数f(x)的解析式;
(2)若关于x的不等式f(x)<kx在x∈(0,1)时恒成立,求实数k的取值范围;
(3)若关于x的不等式f(x)<x+m在x∈(0,1)时恒成立,求实数m的取值范围.
分析 (1)由f(x)解析式得方程,把方程的解代入得关于a,b的方程组,求出a,b即可.
(2)分离参数k>-$\frac{x}{x-2}$在x∈(0,1)时恒成立,求最大值即可;
(3)分离参数,换元求最大值,即可求实数m的取值范围.
解答 解:(1)依已知条件可知方程f(x)-x+12=0即为$\frac{{x}^{2}}{ax+b}$-x+12=0,
因为x1=3,x2=4是上述方程的解,
所以$\left\{\begin{array}{l}{\frac{9}{3a+b}-3+12=0}\\{\frac{16}{4a+b}-4+12=0}\end{array}\right.$,解得a=-2.b=2,
所以函数的解析式为f(x)=-$\frac{{x}^{2}}{x-2}$;
(2)关于x的不等式f(x)<kx在x∈(0,1)时恒成立,
所以k>-$\frac{x}{x-2}$在x∈(0,1)时恒成立,
所以k≥1;
(3)关于x的不等式f(x)<x+m在x∈(0,1)时恒成立,
所以m>-$\frac{{x}^{2}}{x-2}$-x在x∈(0,1)时恒成立,
令2-x=t(t∈(1,2),y=2(t+$\frac{2}{t}$)-6在(1,$\sqrt{2}$)上单调递减,在($\sqrt{2}$,2)上单调递增,
所以4$\sqrt{2}$-6≤y<0,
所以m≥0.
点评 用待定系数法求函数解析式是一种常用的,重要的方法,是基本技能,求参数的范围,利用分离参数法是常用方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.函数y=f(x)的图象如图,则f(x)的定义域是( )
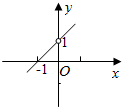
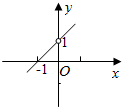
| A. | R | B. | (-∞,1)∪(1,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-1,0) |