题目内容
已知函数f(x)=
,若方程f(x)=a(a∈R)至少有一个实数解,则实数k的取值范围是
|
[-1,0)
[-1,0)
.分析:先求出函数f(x)=log2(x+3)的值域,并画出图象,要使方程f(x)=a(a∈R)至少有一个实数解,则当x∈[1,+∞)时,函数f(x)=1-kx的值域必包含函数f(x)=log2(x+3)的值域在实数集R中的补集,进而求出答案.
解答:解:当x∈(-3,1)时,函数f(x)=log2(x+3)的值域是(-∞,2),
要使方程f(x)=a(a∈R)至少有一个实数解,则当x∈[1,+∞)时,函数f(x)=1-kx的值域必包含[2,+∞),
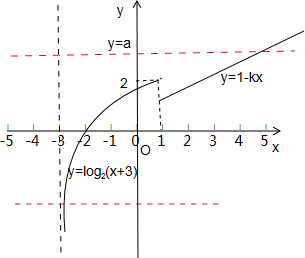 ∴当x∈[1,+∞)时,1-kx≤2恒成立,
∴当x∈[1,+∞)时,1-kx≤2恒成立,
?当x∈[1,+∞)时,0>k≥[-
]max,解得-1≤k<0.
故答案为[-1,0).
要使方程f(x)=a(a∈R)至少有一个实数解,则当x∈[1,+∞)时,函数f(x)=1-kx的值域必包含[2,+∞),
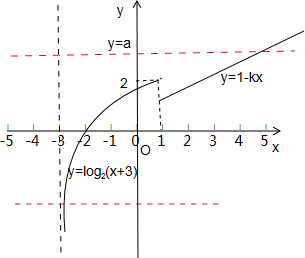 ∴当x∈[1,+∞)时,1-kx≤2恒成立,
∴当x∈[1,+∞)时,1-kx≤2恒成立,?当x∈[1,+∞)时,0>k≥[-
| 1 |
| x |
故答案为[-1,0).
点评:由题意正确得出二函数y=log2(x+3)、y=1-kx的值域间的关系及数形结合是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目