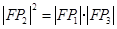题目内容
已知抛物线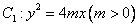 的焦点为
的焦点为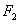 ,其准线与
,其准线与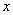 轴交于点
轴交于点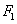 ,以
,以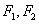 为焦点,离心率为
为焦点,离心率为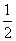 的椭圆
的椭圆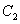 与抛物线
与抛物线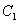 在
在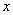 轴上方的一个交点为
轴上方的一个交点为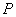 。
。
(1)当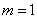 时,求椭圆的标准方程及其右准线的方程;
时,求椭圆的标准方程及其右准线的方程;
(2)用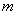 表示
表示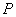 点的坐标;
点的坐标;
(3)是否存在实数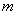 ,使得
,使得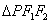 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数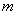 ;若不存在,请说明理由。
;若不存在,请说明理由。
【答案】
解∵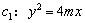 的右焦点
的右焦点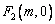 ∴椭圆的半焦距
∴椭圆的半焦距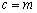 ,又
,又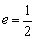 ,∴椭圆的长半轴的长
,∴椭圆的长半轴的长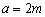 ,短半轴的长
,短半轴的长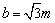 .
椭圆方程为
.
椭圆方程为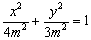 . ---------------4分
. ---------------4分
(Ⅰ)当 时,故椭圆方程为
时,故椭圆方程为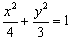 -------5分(直接将m=1的值代入条件求对也给5分)
-------5分(直接将m=1的值代入条件求对也给5分)
右准线方程为: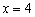 . ---------------6分
. ---------------6分
(Ⅱ)由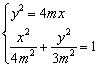 ,解得:
,解得: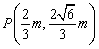 …………10分
…………10分
(Ⅲ)假设存在满足条件的实数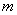 ,
由(Ⅱ)知
,
由(Ⅱ)知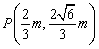
∴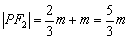 ,
,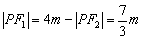 ,又
,又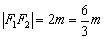 .
.
即 的边长分别是
的边长分别是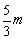 、
、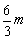 、
、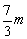 .
---------------14分
.
---------------14分
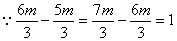 ∴
∴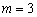 ,
,
故存在实数m使 的边长是连续的自然数。---------------16分
的边长是连续的自然数。---------------16分

练习册系列答案
相关题目
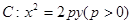 的焦点为
的焦点为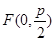 ,准线为
,准线为 ,点
,点 为抛物线C上的一点,且
为抛物线C上的一点,且 的外接圆圆心到准线的距离为
的外接圆圆心到准线的距离为 .
.
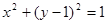 ,过点P作圆F的2条切线分别交
,过点P作圆F的2条切线分别交 轴于点
轴于点 ,求
,求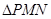 面积的最小值时
面积的最小值时 的值.
的值. 的焦点为
的焦点为 ,点
,点 ,
, 在抛物线上,且
在抛物线上,且 , 则有 ( )
, 则有 ( ) B.
B.
 D.
D.
 的焦点为
的焦点为 ,
, 过
过 轴的垂线交抛物线于
轴的垂线交抛物线于 两点.有下列四个命题:①
两点.有下列四个命题:① 必为直角三角形;②
必为直角三角形;② 必与抛物线相切;④直线
必与抛物线相切;④直线 的焦点为F,准线为
的焦点为F,准线为 ,经过F且斜率为
,经过F且斜率为 的直线与抛物线在
的直线与抛物线在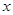 轴上方的部分相交于点A,且AK
轴上方的部分相交于点A,且AK
 的面积是( )
的面积是( ) C
C  D 8
D 8 的焦点为
的焦点为 ,点
,点 ,
, 在抛物线上,且
在抛物线上,且 ,则有( )
,则有( ) B.
B.
 D.
D.