题目内容
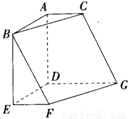
已知多面体ABC-DEFG,AB,AC,AD两两垂直,面ABC//面DEFG,面BEF//面ADGC,AB=AD=DG=2,AC=EF=1,则该多面体的体积为( )
A.2 B.4 C.6 D.8
【答案】
B
【解析】
试题分析:取CD中点H,连接AH,FH,则原多面体分割成棱柱BEF-ADH和棱柱ABC-HFG,两棱柱体积分别为2和2,所以原几何体体积为4
考点:几何体体积
点评:将原几何体分割成两个棱柱,分别求其体积

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
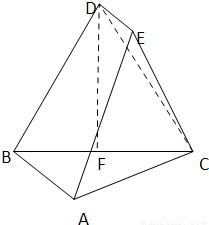
 如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点.
如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点.