题目内容
已知a、b、c分别是△ABC三个内角A、B、C的对边.
(1)若△ABC面积为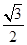 ,c=2,A=60º,求a,b的值;
,c=2,A=60º,求a,b的值;
(2)若acosA=bcosB,试判断△ABC的形状,证明你的结论.
(1)a= ,b=1,(2)直角三角形或等腰三角形
,b=1,(2)直角三角形或等腰三角形
解析试题分析:(1)解三角形问题,一般利用正余弦定理进行边角转化.由面积公式有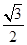 =
= bcsinA=bsin60º,∴b=1.再由余弦定理a2=b2+c2-2bccosA=3,∴a=
bcsinA=bsin60º,∴b=1.再由余弦定理a2=b2+c2-2bccosA=3,∴a= .(2)由正弦定理得2RsinA=a,2RsinB=b,∴2RsinAcosA=2RsinBcosB,即sin2A=sin2B,由已知A、B为三角形内角,∴A+B=90º或A=B.∴△ABC为直角三角形或等腰三角形.本题也可从余弦定理出发:
.(2)由正弦定理得2RsinA=a,2RsinB=b,∴2RsinAcosA=2RsinBcosB,即sin2A=sin2B,由已知A、B为三角形内角,∴A+B=90º或A=B.∴△ABC为直角三角形或等腰三角形.本题也可从余弦定理出发: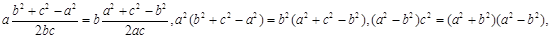 所以
所以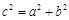 或
或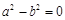 .
.
解:(1)由已知得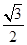 =
= bcsinA=bsin60º,∴b=1.
bcsinA=bsin60º,∴b=1.
由余弦定理a2=b2+c2-2bccosA=3,∴a= .
.
(2)由正弦定理得2RsinA=a,2RsinB=b,
∴2RsinAcosA=2RsinBcosB,即sin2A=sin2B,由已知A、B为三角形内角,
∴A+B=90º或A=B.∴△ABC为直角三角形或等腰三角形
考点:正余弦定理

练习册系列答案
相关题目
 中,
中, ,且
,且 .
. ; (2)求
; (2)求 .
. 是
是 的三个内角,且其对边分别为
的三个内角,且其对边分别为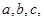 且
且
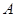 的大小;
的大小; 求
求 =(-cos
=(-cos ,sin
,sin =(cos
=(cos ,且
,且 .
. 中,角
中,角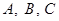 所对的边分别为
所对的边分别为 ,且
,且 .
. 的大小;
的大小; ,求
,求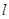 的取值范围.
的取值范围. 中,
中,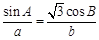 .
.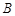 的值;
的值;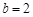 ,求
,求 中,角
中,角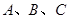 所对的边分别为
所对的边分别为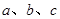 ,
,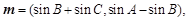
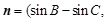
 ),且
),且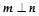 .
.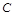 的大小;
的大小;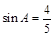 ,求
,求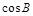 的值.
的值. 中,角
中,角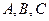 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, ,
, ;
; ,
, ,求
,求 ,b=5,求sin Bsin C的值.
,b=5,求sin Bsin C的值.