题目内容
已知定义在I上的函数f（x）的导函数为f'（x），满足0＜f'（x）＜2且f'（x）≠1，常数C1是方程f（x）-x=0的实根，常数C2是方程f（x）-2x=0的实根．（1）若对任意[a，b]⊆I，存在xo∈（a，b）使等式
| f(b)-f(a) | b-a |
（2）求证：当x＞c2时，总有f（x）＜2x；
（3）若|x1-c1|＜1，|x2-c1|＜1，求证：|f（x1）-f（x2）|＜4．
分析：（1）假设方程f（x）-x=0存在另一根，则利用条件可得出矛盾；（2）构造函数F（x）=f（x）-2x，可得F（x）在（c2，+∞）单调递减，从而可证；（3）不妨设x1≤x2，①当x1=x2时，显然成立．②当x1＜x2时，利用（Ⅱ）的结论可证．
解答：证明：（1）假设存在另一根m（m≠c1）即f（m）=m，f（c1）=c1，则
=
=1，与
=f’（x0）≠1矛盾，所以假设错误，原命题结论正确．
（2）设F（x）=f（x）-2x，则F’（x）=f’（x）-2＜0，∴F（x）在（c2，+∞）单调递减，
∴F（x）＜F（c2）=f（c2）-2c2=0∴f（x）＜2x
（3）不妨设x1≤x2，①当x1=x2时，显然成立．
②当x1＜x2时，由（Ⅱ）知f（x1）-2x1＞f（x2）-2x2，∴f（x1）-f（x2）＞2x1-2x2
又∵f’（x）＞0，∴f（x2）-f（x1）＞0
∴|f（x2）-f（x1）|＜2|x2-x1|=2|x2-c1-（x1-c1）|≤2|x2-c1|+2|x1-c1|≤2+2=4，
所以|f（x2）-f（x1）|≤4．
| f(m)-f(c1) |
| m-c1 |
| m-c1 |
| m-c1 |
| f(m)-f(c1) |
| m-c1 |
（2）设F（x）=f（x）-2x，则F’（x）=f’（x）-2＜0，∴F（x）在（c2，+∞）单调递减，
∴F（x）＜F（c2）=f（c2）-2c2=0∴f（x）＜2x
（3）不妨设x1≤x2，①当x1=x2时，显然成立．
②当x1＜x2时，由（Ⅱ）知f（x1）-2x1＞f（x2）-2x2，∴f（x1）-f（x2）＞2x1-2x2
又∵f’（x）＞0，∴f（x2）-f（x1）＞0
∴|f（x2）-f（x1）|＜2|x2-x1|=2|x2-c1-（x1-c1）|≤2|x2-c1|+2|x1-c1|≤2+2=4，
所以|f（x2）-f（x1）|≤4．
点评：本题主要考查函数与不等式的综合，考查构造函数研究函数的单调性，有一定的综合性．
练习册系列答案
相关题目
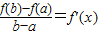成立．证明：方程f（x）-x=0有且只有一个实根；