题目内容
14、（不等式选讲选做题）|x-3|+|x-5|≥4的解集是
{x|x≤2，或x≥6}
．分析：利用查绝对值的意义，满足|x-3|+|x-5|=4的x值为2和6，故满足|x-3|+|x-5|≥4 的x值为 x≤2，或x≥6．
解答：解：∵|x-3|+|x-5|表示数轴上的x对应点到3和5对应点的距离之和，满足|x-3|+|x-5|=4的x值为
2和6，故满足|x-3|+|x-5|≥4 的x值为 x≤2，或x≥6，故不等式的解集为{x|x≤2，或x≥6}，
故答案为：{x|x≤2，或x≥6}．
2和6，故满足|x-3|+|x-5|≥4 的x值为 x≤2，或x≥6，故不等式的解集为{x|x≤2，或x≥6}，
故答案为：{x|x≤2，或x≥6}．
点评：本题考查绝对值的意义，绝对值不等式的解法，判断满足|x-3|+|x-5|=4的x值为2和6，是解题的关键．
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
相关题目
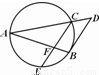
，则线段CD的长为 ．
）的直角坐标是 ．
，则线段CD的长为 ．
）的直角坐标是 ．
，则线段CD的长为 ．
）的直角坐标是 ．
，则线段CD的长为 ．
）的直角坐标是 ．
，则线段CD的长为 ．
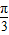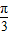）的直角坐标是 ．