题目内容
函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性等,请选择适当的探究顺序,研究函数f(x)=| 1-sinx |
| 1+sinx |
分析:本题研究的顺序为:先研究定义域、奇偶性、周期性,再研究函数的单调性、值域,最后画出图形.
解答:解:①∵
∴f(x)的定义域为R;(2分)
②∵f(-x)=
+
=
+
=f(x),
∴f(x)为偶函数;(4分)
③∵f(x+π)=
+
=
+
=f(x),
∴f(x)是周期为π的周期函数;(6分)
④当x∈[0,
]时,f(x)=
=
=2cos
,
∴当x∈[0,
]时,f(x)单调递减;当x∈[
,π]时,
f(x)=
=
=
=2sin
,
f(x)单调递增;又∵f(x)是周期为π的偶函数,
∴f(x)在[kπ+
,kπ+π]上单调递增,在[kπ,kπ+
]上单调递减(k∈Z);(8分)
⑤∵当x∈[0,
]时,f(x)=2cos
∈[
,2];
当x∈[
,π]时,f(x)=2sin
∈[
,2].
∴f(x)的值域为[
,2];(10分)
⑥由以上性质可得:f(x)在[-π,π]上的图象如图所示:
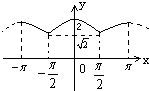
(12分)
|
∴f(x)的定义域为R;(2分)
②∵f(-x)=
| 1-sin(-x) |
| 1+sin(-x) |
| 1+sinx |
| 1-sinx |
∴f(x)为偶函数;(4分)
③∵f(x+π)=
| 1-sin(x+π)? |
| 1+sin(x+π)? |
| 1-sinx |
| 1+sinx |
∴f(x)是周期为π的周期函数;(6分)
④当x∈[0,
| π |
| 2 |
(
|
| 2+2|cosx| |
| x |
| 2 |
∴当x∈[0,
| π |
| 2 |
| π |
| 2 |
f(x)=
(
|
| 2+2|cosx| |
| 2-2cosx |
| x |
| 2 |
f(x)单调递增;又∵f(x)是周期为π的偶函数,
∴f(x)在[kπ+
| π |
| 2 |
| π |
| 2 |
⑤∵当x∈[0,
| π |
| 2 |
| x |
| 2 |
| 2 |
当x∈[
| π |
| 2 |
| x |
| 2 |
| 2 |
∴f(x)的值域为[
| 2 |
⑥由以上性质可得:f(x)在[-π,π]上的图象如图所示:

(12分)
点评:本题考查二倍角公式的应用,正弦函数、余弦函数的图象和性质,以及y=Asin(ωx+φ)的图象及性质.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
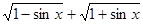 的性质,并在此基础上,作出其在
的性质,并在此基础上,作出其在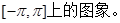
 的性质,并在此基础上,作出其在
的性质,并在此基础上,作出其在 上的图像.
上的图像.