题目内容

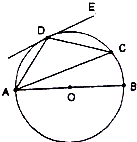如图，AB是圆O的直径，C、D是圆上的点，∠BAC=20°，弧
AD
和弧
DC
的长相等，DE是圆O的切线，则∠EDC=（　　）
分析：根据∠BAC=20°，弧
AD
和弧
DC
的长相等，求得弧
DC
所对的圆心角为
1
2
(180°-2×20°)=70°，再利用DE是圆O的切线，即可求得∠EDC．
解答：解：∵∠BAC=20°，弧
AD
和弧
DC
的长相等，
∴弧
DC
所对的圆心角为
1
2
(180°-2×20°)=70°
∵DE是圆O的切线，∴∠EDC=
1
2
×70°=35°
故选D．
点评：本题考查圆的切线，考查圆周角定理，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
（理科）如图的多面体是底面为平行四边形的直四棱柱ABCD-A1B1C1D1，经平面AEFG所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．
精英家教网
（Ⅰ）求证：BD⊥平面ADG；
（Ⅱ）求平面AEFG与平面ABCD所成锐二面角的余弦值．

（文科）如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．
（Ⅰ）求证：AF⊥平面CBF；
（Ⅱ）设FC的中点为M，求证：OM∥平面DAF．
精英家教网
精英家教网如图，直三棱柱的一个底面ABC内接于圆O，AB是圆O的直径．
（1）求证：平面ACD⊥平面ADE；
（2）若AB=2，BC=1，tan∠EAB=
3
2
，求几何体EDABC的体积V．

（理科）如图的多面体是底面为平行四边形的直四棱柱ABCD-A1B1C1D1，经平面AEFG所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．

（Ⅰ）求证：BD⊥平面ADG；
（Ⅱ）求平面AEFG与平面ABCD所成锐二面角的余弦值．

（文科）如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．
（Ⅰ）求证：AF⊥平面CBF；
（Ⅱ）设FC的中点为M，求证：OM∥平面DAF．
（理科）如图的多面体是底面为平行四边形的直四棱柱ABCD-A1B1C1D1，经平面AEFG所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．

（Ⅰ）求证：BD⊥平面ADG；
（Ⅱ）求平面AEFG与平面ABCD所成锐二面角的余弦值．

（文科）如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．
（Ⅰ）求证：AF⊥平面CBF；
（Ⅱ）设FC的中点为M，求证：OM∥平面DAF．

 A．（参数方程与极坐标）

直线与直线的夹角大小为         

 

B．（不等式选讲）要使关于x的不等式在实数

范围内有解，则A的取值范围是                  

C．（几何证明选讲） 如图所示，在圆O中，AB是圆O的直

径AB =8,E为OB．的中点，CD过点E且垂直于AB,

EF⊥AC,则

CF•CA=            

 

 

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网