题目内容
13．求下列函数的周期：（1）y=sin3x，x∈R；
（2）y=3sin$\frac{x}{4}$，x∈R；
（3）y=2sin（2x-$\frac{π}{6}$）．
分析 由条件利用函数y=Asin（ωx+φ）的周期为$\frac{2π}{ω}$，得出结论．
解答 解：（1）函数y=sin3x，x∈R的最小正周期为$\frac{2π}{3}$；
（2）函数y=3sin$\frac{x}{4}$，x∈R的最小正周期为$\frac{2π}{\frac{1}{4}}$=8π；
（3）函数y=2sin（2x-$\frac{π}{6}$）的最小正周期为$\frac{2π}{2}$=π．
点评 本题主要考查函数y=Asin（ωx+φ）的周期性，利用了函数y=Asin（ωx+φ）的周期为$\frac{2π}{ω}$，属于基础题．
练习册系列答案
相关题目
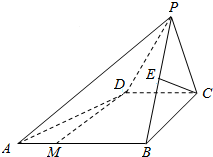如图，已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，AB=BC=PB=PC=2CD=2，侧面PBC⊥底面ABCD，点M在AB上，且AM：MB=1：2，E为PB的中点．