题目内容
设全集U={1,2,3,4,5,6},集合P={1,2,3,4},Q={3,4,5},则P∩(∁UQ)= ( )
| A.{1,2,3,4,6} | B.{1,2,3,4,5} | C.{1,2,5} | D.{1,2} |
D
解析试题分析:找出全集U中不属于Q的元素,确定出Q的补集,找出P与Q补集的公共元素,即可确定出所求的集合.解:∵全集U={1,2,3,4,5,6},Q={3,4,5},∴CUQ={1,2,6},又P={1,2,3,4},则P∩(CUQ)={1,2}.故答案为D
考点:集合的运算
点评:此题考查了交、并、补集的混合运算,熟练掌握交、并、补集的定义是解本题的关键.

练习册系列答案
相关题目
集合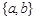 的子集有 ( )
的子集有 ( )
| A.2个 | B.3个 | C.4个 | D.5个 |
已知集合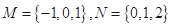 ,则如图所示韦恩图中的阴影部分所表示的集合为
,则如图所示韦恩图中的阴影部分所表示的集合为
A. | B.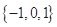 | C.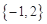 | D.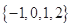 |
设集合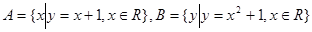 ,则
,则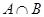 =( )
=( )
A.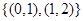 | B.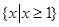 | C.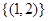 | D.R |
已知集合A={x||x|≤2,x∈R},B={x| ≤2,x∈Z},则A∩B=
≤2,x∈Z},则A∩B=
| A.(0,2) | B.[0,2] | C.{0,2} | D.{0,1,2} |
设全集U={1,2,3,4},则集合A="{1," 3},则CUA=( )
| A.{1, 4} | B.{2, 4} | C.{3, 4} | D.{2, 3} |
若集合 则集合
则集合 ( )
( )
A.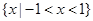 | B. |
C.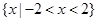 | D. |
集合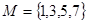 ,
, 则
则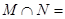 ( )。
( )。
A.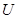 | B.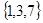 | C.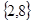 | D. |
 A)∩B等于
A)∩B等于