题目内容
若样本a1,a2,…,an的平均数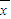 =5,方差s2=0.025,则样本4a1、4a2,…,4an的平均数是 ,方差是 .
=5,方差s2=0.025,则样本4a1、4a2,…,4an的平均数是 ,方差是 .
【答案】分析:考虑到样本4a1、4a2,…,4an的各个数据是原数据的4倍,充分利用两者的关系结合方差的计算公式计算即可.
解答:解:∵样本a1,a2,…,an的平均数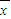 =5,
=5,
∴4a1、4a2,…,4an的平均数=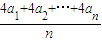 =
=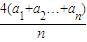 =4×5=20;
=4×5=20;
4a1、4a2,…,4an的方差=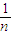 [(4a1-20)2+(4a2-20)2+…+(4an-20)2]
[(4a1-20)2+(4a2-20)2+…+(4an-20)2]
=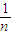 {16×[(a1-5)2+(a2-5)2+…+(an-5)2]}
{16×[(a1-5)2+(a2-5)2+…+(an-5)2]}
=16×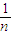 [(a1-5)2+(a2-5)2+…+(an-5)2]
[(a1-5)2+(a2-5)2+…+(an-5)2]
=16×0.025=0.4.
故填20;0.4.
点评:本题考查平均数与方差的定义:一般地设n个数据,x1,x2,…xn的平均数为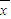 ,则方差S2=
,则方差S2=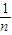 [(x1-
[(x1-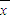 )2+(x2-
)2+(x2-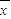 )2+…+(xn-
)2+…+(xn-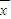 )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
解答:解:∵样本a1,a2,…,an的平均数
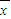 =5,
=5,∴4a1、4a2,…,4an的平均数=
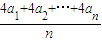 =
=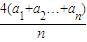 =4×5=20;
=4×5=20;4a1、4a2,…,4an的方差=
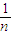 [(4a1-20)2+(4a2-20)2+…+(4an-20)2]
[(4a1-20)2+(4a2-20)2+…+(4an-20)2]=
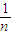 {16×[(a1-5)2+(a2-5)2+…+(an-5)2]}
{16×[(a1-5)2+(a2-5)2+…+(an-5)2]}=16×
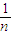 [(a1-5)2+(a2-5)2+…+(an-5)2]
[(a1-5)2+(a2-5)2+…+(an-5)2]=16×0.025=0.4.
故填20;0.4.
点评:本题考查平均数与方差的定义:一般地设n个数据,x1,x2,…xn的平均数为
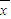 ,则方差S2=
,则方差S2=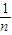 [(x1-
[(x1-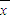 )2+(x2-
)2+(x2-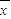 )2+…+(xn-
)2+…+(xn-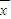 )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立. 
练习册系列答案
相关题目