题目内容
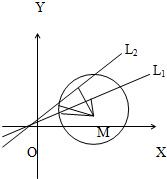 如图,已知两条直线L1:2x-3y+2=0,L2:3x-2y+3=0.有一动圆(圆心和半径都在变动)与L1,L2都相交,并且L1,L2被截在圆内的两条线段的长度分别是定值26,24,求圆心M的轨迹方程,并说出轨迹的名称.
如图,已知两条直线L1:2x-3y+2=0,L2:3x-2y+3=0.有一动圆(圆心和半径都在变动)与L1,L2都相交,并且L1,L2被截在圆内的两条线段的长度分别是定值26,24,求圆心M的轨迹方程,并说出轨迹的名称.
分析:设圆心M的坐标为(x,y),欲求其轨迹方程,即寻找其坐标间的关系,根据弦、弦心距、半径三者之间的关系及点到直线的距离公式即可得到.
解答:解:设圆心M的坐标为(x,y),圆的半径为r,
点M到L1,L2的距离分别为d1,d2
根据弦、弦心距、半径三者之间的关系,有
d12+(
)2=r2,
d22+(
)2=r2.
得d22-d12=52.
根据点到直线的距离公式,得
d1=
,d2=
代入上式,
得方程(
)2-(
)2=25
化简得x2+2x+1-y2=65.即
-
=1.
所以轨迹是双曲线.
点M到L1,L2的距离分别为d1,d2
根据弦、弦心距、半径三者之间的关系,有
d12+(
| 26 |
| 2 |
d22+(
| 24 |
| 2 |
得d22-d12=52.
根据点到直线的距离公式,得
d1=
| |2x-3y+2| | ||
|
| |3x-2y+3| | ||
|
得方程(
| 2x-3y+2 | ||
|
| 3x-2y+3 | ||
|
化简得x2+2x+1-y2=65.即
| (x+1)2 |
| 65 |
| y2 |
| 65 |
所以轨迹是双曲线.
点评:求曲线的轨迹方程是解析几何的基本问题.求符合某种条件的动点的轨迹方程,其实质就是利用题设中的几何条件,用“坐标化”将其转化为寻求变量间的关系.

练习册系列答案
相关题目
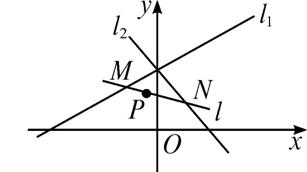
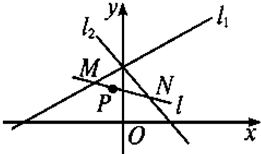 如图,已知两条直线l1:x-3y+12=0,l2:3x+y-4=0,过定点P(-1,2)作一条直线l,分别与l1,l2交于M、N两点,若P点恰好是MN的中点,求直线l的方程.
如图,已知两条直线l1:x-3y+12=0,l2:3x+y-4=0,过定点P(-1,2)作一条直线l,分别与l1,l2交于M、N两点,若P点恰好是MN的中点,求直线l的方程.