题目内容
教科书中有如下的对数运算性质:loga(MN)=logaM+logaN(a>0,a≠1,M>0,N>0).已知f(x)、g(x)互为反函数(x∈R),若函数g(x)有性质:对于任意的实数m,n,有g(mn)=g(m)+g(n),通过类比的思想,猜想函数f(x)性质:________.
对于任意的实数m,n,有f(m+n)=f(m)•f(n)
分析:指数函数是对数函数的反函数,类比于数函数具有a m+n=am+an的性质可写出结果.
解答:若函数g(x)有性质:对于任意的实数m,n,有g(mn)=g(m)+g(n),
对数函数是g(x)得特例,对数函数与指数函数互为反函数,且指数函数具有a m+n=am+an的性质
因此猜想函数f(x)性质对于任意的实数m,n,有f(m+n)=f(m)•f(n)
故答案为:对于任意的实数m,n,有f(m+n)=f(m)•f(n)
点评:本题考查类比推理,借用了指数函数、对数函数性质.
分析:指数函数是对数函数的反函数,类比于数函数具有a m+n=am+an的性质可写出结果.
解答:若函数g(x)有性质:对于任意的实数m,n,有g(mn)=g(m)+g(n),
对数函数是g(x)得特例,对数函数与指数函数互为反函数,且指数函数具有a m+n=am+an的性质
因此猜想函数f(x)性质对于任意的实数m,n,有f(m+n)=f(m)•f(n)
故答案为:对于任意的实数m,n,有f(m+n)=f(m)•f(n)
点评:本题考查类比推理,借用了指数函数、对数函数性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

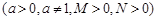 .已知
.已知 、
、 互为反函数
互为反函数 ,若函数
,若函数 有性质:对于任意的实数
有性质:对于任意的实数 ,有
,有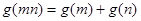 ,通过类比的思想,猜想函数
,通过类比的思想,猜想函数 性质:___________________________________________.
性质:___________________________________________.