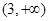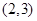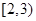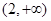题目内容
已知函数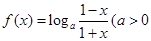 且
且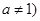 的图象经过点
的图象经过点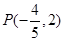 .
.
(1)求函数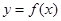 的解析式;
的解析式;
(2)设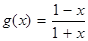 ,用函数单调性的定义证明:函数
,用函数单调性的定义证明:函数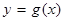 在区间
在区间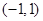 上单调递减;
上单调递减;
(3)解不等式: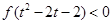 .
.
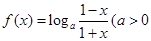 且
且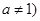 的图象经过点
的图象经过点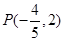 .
. (1)求函数
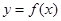 的解析式;
的解析式;(2)设
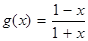 ,用函数单调性的定义证明:函数
,用函数单调性的定义证明:函数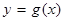 在区间
在区间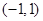 上单调递减;
上单调递减;(3)解不等式:
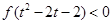 .
.(1)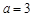 ,(2)详见解析,(3)
,(2)详见解析,(3)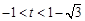 或
或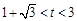 .
.
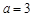 ,(2)详见解析,(3)
,(2)详见解析,(3)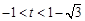 或
或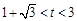 .
.试题分析:(1)求函数
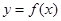 的解析式,只需确定
的解析式,只需确定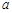 的值即可,由函数
的值即可,由函数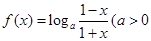 且
且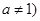 的图象经过点
的图象经过点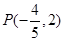 ,得
,得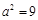 ,再由
,再由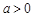 得
得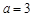 ,(2)用函数单调性的定义证明单调性,一设
,(2)用函数单调性的定义证明单调性,一设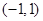 上的任意两个值,二作差,三因式分解确定符号,(3)解不等式,一可代入解析式,转化为解对数不等式,需注意不等号方向及真数大于零隐含条件,二利用函数单调性,去“
上的任意两个值,二作差,三因式分解确定符号,(3)解不等式,一可代入解析式,转化为解对数不等式,需注意不等号方向及真数大于零隐含条件,二利用函数单调性,去“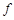 ”,注意定义域.
”,注意定义域.试题解析:(1)
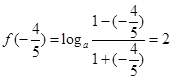 ,解得:
,解得: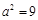 ∵
∵ 且
且 ∴
∴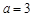 ; 3分
; 3分(2)设
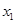 、
、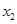 为
为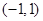 上的任意两个值,且
上的任意两个值,且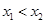 ,则
,则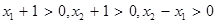
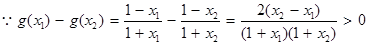 6分
6分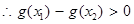 ,
,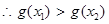
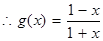 在区间
在区间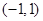 上单调递减. 8分
上单调递减. 8分(3)方法(一):
由
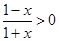 ,解得:
,解得: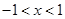 ,即函数
,即函数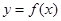 的定义域为
的定义域为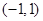 ; 10分
; 10分先研究函数
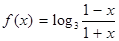 在
在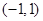 上的单调性.
上的单调性.可运用函数单调性的定义证明函数
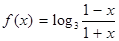 在区间
在区间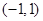 上单调递减,证明过程略.
上单调递减,证明过程略. 或设
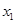 、
、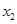 为
为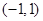 上的任意两个值,且
上的任意两个值,且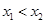 ,
,由(2)得:
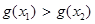
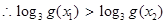 ,即
,即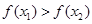
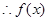 在区间
在区间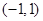 上单调递减. 12分
上单调递减. 12分再利用函数
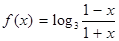 的单调性解不等式:
的单调性解不等式: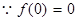 且
且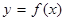 在
在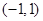 上为单调减函数.
上为单调减函数.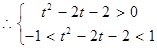 , 13分
, 13分即
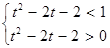 ,解得:
,解得: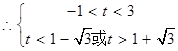
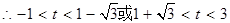 . 15分
. 15分方法(二):
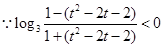
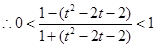 10分
10分由
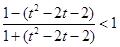 得:
得: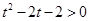 或
或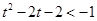 ;由
;由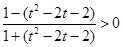 得:
得: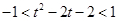 ,
,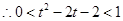 13分
13分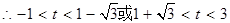 . 15分
. 15分
练习册系列答案
相关题目
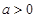 ,函数
,函数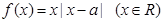 .
.
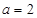 时,画出函数
时,画出函数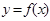 的大致图像;
的大致图像;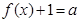 解的个数.
解的个数.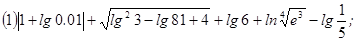
 ,求它的定义域和值域。
,求它的定义域和值域。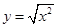 和
和 是同一函数;②函数
是同一函数;②函数 的定义域为
的定义域为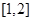 ,则函数
,则函数 的定义域为
的定义域为 ;③函数
;③函数 的递增区间为
的递增区间为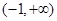 ;④若函数
;④若函数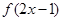 的最大值为3,那么
的最大值为3,那么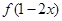 的最小值就是
的最小值就是 .
. 的定义域是_________________________
的定义域是_________________________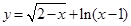 的定义域为 .
的定义域为 .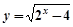 的定义域为 .
的定义域为 .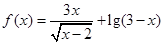 的定义域是( )
的定义域是( )