题目内容

15．如图，长方形木块上底面有一点E，在上底面画一条过点E的线段l，使l与AE垂直．

分析 连接A1E，再过点E作直线l，当直线l垂直于A1E时，必有l垂直于AE，由线面垂直的判定定理先证明l⊥平面AA1E，即可证明l⊥AE．

解答 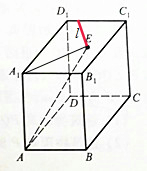解：如图，连接A1E，再过点E作直线l，当直线l垂直于A1E时，必有l垂直于AE．
由做法可知，直线l⊥A1E，
又l?上底面A1B1C1D1，AA1⊥上底面A1B1C1D1，即有：AA1⊥l，
又A1E∩AA1=A1，
所以，l⊥平面AA1E，
由AE?平面AA1E，
故有：l⊥AE．

点评 本题主要考查了直线与平面垂直的性质，考查了空间想象能力和推理论证能力，属于基本知识的考查．

练习册系列答案
相关题目
5．在△ABC中，已知$\overrightarrow{AB}•\overrightarrow{AC}=9，sinB=cosAsinC$，S△ABC=6，P为线段AB上的点，且$\overrightarrow{CP}=x\frac{{\overrightarrow{CA}}}{{|{\overrightarrow{CA}}|}}+y\frac{{\overrightarrow{CB}}}{{|{\overrightarrow{CB}}|}}$，
则$\overrightarrow{CP}•\overrightarrow{BP}$的最小值为$-\frac{64}{25}$．
6．若二次函数f（x）=ax2+bx+c（a，b，c∈R）满足f（-1）=0，且对任意实数x，均有x-1≤f（x）≤x2-3x+3恒成立．
（1）求函数的解析式；
（2）若关于x的不等式f（x）≤nx-1的解集非空，求实数n的取值集合A．
3．已知a，b，c均为直线，α，β为平面，下面关于直线与平面关系的命题：
（1）任意给定一条直线与一个平面α，则平面α内必存在与a垂直的直线；
（2）a∥β，β内必存在与a相交的直线；
（3）α∥β，a?α，b?β，必存在与a，b都垂直的直线；
（4）α⊥β，α∩β=c，a?α，b?β，若a不垂直c，则a不垂直b．
其中真命题的个数为（　　）
A．1B．2C．3D．4
10．在极坐标系（ρ，θ）（0≤θ＜2π）中，曲线ρ（2cosθ-sinθ）=3与ρ（cosθ+2sinθ）=-1的交点的极坐标为$（\sqrt{2}，\frac{7π}{4}）$．
20．已知函数y=mx与y=ex在[-1，+∞）上无交点，求m的取值范围．
1．函数f（x）的定义域为[-1，1]，图象如图1所示；函数g（x）的定义域为[-2，2]，图象如图2所示，方程f（g（x））=0有m个实数根，方程g（f（x））=0有n个实数根，则m+n=（　　） 
A．6B．8C．10D．12
18．已知曲线C的方程为$\sqrt{（x+1）^{2}+{y}^{2}}$+$\sqrt{（x-1）^{2}+{y}^{2}}$=4，经过点（-1，0）作斜率为k的直线l，l与曲线C交于A、B两点，l与直线x=-4交于点D，O是坐标原点．
（Ⅰ）若$\overrightarrow{OA}+\overrightarrow{OD}=2\overrightarrow{OB}$，求证：k2=$\frac{5}{4}$；
（Ⅱ）是否存在实数k，使△AOB为锐角三角形？若存在，求k的取值范围，若不存在，请说明理由．
19．在极坐标系中，已知点P（2，$\frac{π}{3}$），Q为曲线ρ=cosθ上任意一点，则|PQ|的最小值为$\frac{\sqrt{13}-1}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网