题目内容
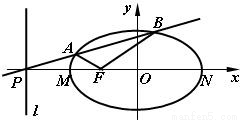
如图,设F是椭圆 的左焦点,直线l为左准线,直线l与x轴交于P点,MN为椭圆的长轴,已知
的左焦点,直线l为左准线,直线l与x轴交于P点,MN为椭圆的长轴,已知 ,且
,且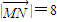 .
.(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点P作直线与椭圆交于A、B两点,求△ABF面积的最大值.
【答案】分析:(Ⅰ)利用椭圆的长轴求得椭圆方程中的a,利用椭圆的定义和 求得离心率,进而求得c,则b的值可得,最后求得椭圆的标准方程.
求得离心率,进而求得c,则b的值可得,最后求得椭圆的标准方程.
(Ⅱ)设出AB的方程,代入椭圆方程整理后利用韦达定理表示出yA+yB和yAyB,进而根据S△ABF=S△PBF-S△PAF|表示出△ABF面积利用基本不等式求得面积的最大值.
解答:解:(Ⅰ)由题意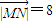 ,得2a=8,∴a=4.
,得2a=8,∴a=4.
又 ,∴
,∴
∴c=2,b2=a2-c2=12.
∴椭圆的标准方程为 .
.
(Ⅱ)设过P点的直线AB方程为x=my-8,
代入椭圆方程整理得(3m2+4)y2-48my+144=0,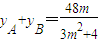 ,
, .
.
而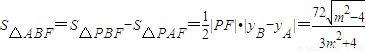 .
.
即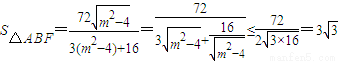 .
.
当且仅当 ,即
,即 时等号成立,且满足△>0.
时等号成立,且满足△>0.
∴△ABF面积的最大值是 .
.
点评:本题主要考查了椭圆的简单性质,直线与椭圆的关系.解题最后注意对所求的m的值代入判别式进行验证.保证答题的严密性.
 求得离心率,进而求得c,则b的值可得,最后求得椭圆的标准方程.
求得离心率,进而求得c,则b的值可得,最后求得椭圆的标准方程.(Ⅱ)设出AB的方程,代入椭圆方程整理后利用韦达定理表示出yA+yB和yAyB,进而根据S△ABF=S△PBF-S△PAF|表示出△ABF面积利用基本不等式求得面积的最大值.
解答:解:(Ⅰ)由题意
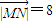 ,得2a=8,∴a=4.
,得2a=8,∴a=4.又
 ,∴
,∴
∴c=2,b2=a2-c2=12.
∴椭圆的标准方程为
 .
.(Ⅱ)设过P点的直线AB方程为x=my-8,
代入椭圆方程整理得(3m2+4)y2-48my+144=0,
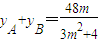 ,
, .
.而
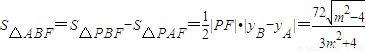 .
.即
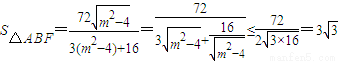 .
.当且仅当
 ,即
,即 时等号成立,且满足△>0.
时等号成立,且满足△>0.∴△ABF面积的最大值是
 .
.点评:本题主要考查了椭圆的简单性质,直线与椭圆的关系.解题最后注意对所求的m的值代入判别式进行验证.保证答题的严密性.

练习册系列答案
相关题目
 的左焦点,直线l为对应的准线,直线l与x轴交于P点,线段MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|.
的左焦点,直线l为对应的准线,直线l与x轴交于P点,线段MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|.
 的左焦点,直线l为左准线,直线l与x轴交于P点,MN为椭圆的长轴,已知
的左焦点,直线l为左准线,直线l与x轴交于P点,MN为椭圆的长轴,已知 ,且
,且 .
.
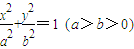 的左焦点,直线l为对应的准线,直线l与x轴交于P点,线段MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|.
的左焦点,直线l为对应的准线,直线l与x轴交于P点,线段MN为椭圆的长轴,已知|MN|=8,且|PM|=2|MF|.