题目内容
已知动点P与双曲线x2-y2=1的两个焦点F1,F2的距离之和为 定值,
定值,
(1)求动点P的轨迹方程;
(2)设M(0,-1),若斜率为k(k≠0)的直线l与P点的轨迹交于不同的两点A、B,若要使|MA|=|MB|,试求k的取值范围.
【答案】
(1)∵x2-y2=1,∴c=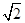 . PF1|+|PF2|=
. PF1|+|PF2|=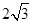
 a=
a=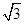 b=1
b=1
 ∴P点的轨迹方程为
∴P点的轨迹方程为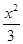 +y2=1.
+y2=1.
(2)设l:y=kx+m(k≠0),则由,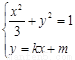 将②代入①得:(1+3k2)x2+6kmx+3(m2-1)=0 (*)
将②代入①得:(1+3k2)x2+6kmx+3(m2-1)=0 (*)
设A(x1,y1),B(x2,y2),则AB中点Q(x0,y0)的坐标满足
Q(-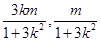 ) ∵|MA|=|MB|,∴M在AB的中垂线上,
) ∵|MA|=|MB|,∴M在AB的中垂线上,
∴klkAB=-1 ,解得m=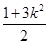 …③ 又由于(*)式有两个实数根,知△>0,
…③ 又由于(*)式有两个实数根,知△>0,
即 (6km)2-4(1+3k2)[3(m2-1)]=12(1+3k2-m2)>0 ④ ,将③代入④得
12[1+3k2-(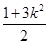 )2]>0,解得-1<k<1,由k≠0,
)2]>0,解得-1<k<1,由k≠0,
∴k的取值范围是k∈(-1,0)∪(0,1).
【解析】略

练习册系列答案
相关题目