Question

已知函数f(x)=

(x2-2ax)ex x＞0 bx x≤0

，x=

2

是函数y=f（x）的极值点．
（I）求实数a的值；
（II）若方程f（x）-m=0有两个不相等的实数根，求实数m的取值范围．

Answer 1

分析：（I）先求导函数f′（x），根据极值的定义可知f′(

2

)=0，建立等式关系，解之即可；
（II）先根据函数的单调性研究出函数在（0，+∞）上的值域，然后要使方程f（x）-m=0有两不相等的实数根，即函数y=f（x）的图象与直线y=m有两个不同的交点，讨论b与0的大小，结合图象进行求解即可．

解答：解：（I）x＞0时，f（x）=（x²-2ax）e^x
∴f′（x）=（2x-2a）e^x+（x²-2ax）e^x=[x²+2（1-a）x-2a]e^x（2分）
由已知，f′(

2

)=0，
∴[2+2

2

(1-a)-2a]e

2

=0，
∴2+2

2

-2a-2

2

a=0，得a=1
（II）由（I）x＞0时，f（x）=（x²-2x）e^x，
∴f′（x）=（2x-2）e^x+（x²-2x）e^x=（x²-2）e^x
令f'（x）=0得x=

2

（x=-

2

舍去）
当x＞0时

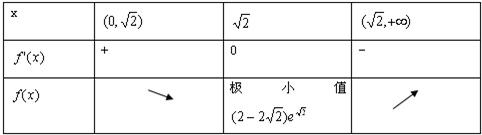
所以，当x∈(0，

2

)时，f（x）单调递减，f(x)∈((2-2

2

)e

2

，0)
当x∈(

2

，+∞)时，f（x）单调递减，f（x）∈((2-2

2

)e

2

，+∞)
∴x＞0时，f（x）∈((2-2

2

)e

2

，+∞)
要使方程f（x）-m=0有两不相等的实数根，即函数y=f（x）的图象与直线y=m有两个不同的交点．
（1）当b＞0时，m=0或m=(2-

2

)e

2

（2）当b=0时，m∈((2-2

2

)e

2

，0)
（3）当b＜0时，m((2-2

2

)e

2

，+∞)

点评：本题主要考查函数与导数的基本知识，几何意义及其应用，同时考查学生分类讨论思想、函数与方程思想、数形结合思想以及转化与归化的能力．