Question

（2012•焦作模拟）在公比为2的等比数列{a_n}中，a₂与a₄的等差中项是5

3

．
（Ⅰ）求a₁的值；
（Ⅱ）若函数y=|a₁|sin（

π

4

x+?），|?|＜π的一部分图象如图所示，M（-1，|a₁|），N(3，-

3

)为图象上的两点，设∠MPN=β，其中P与坐标原因O重合，0≤β≤π，求tan（φ-β）的值．

Answer 1

分析：（Ⅰ）直接利用等比数列．以及等差中项求出a₁．
（Ⅱ）利用（Ⅰ）和函数的图象求出函数的解析式，通过余弦定理求出β的值，然后利用两角和与差的正切函数求出结果即可．

解答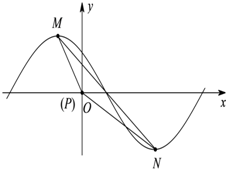：解：（Ⅰ）∵公比为2的等比数列{a_n}中，a₂与a₄的等差中项是5

3

，
∴2a₁+8a₁=10

3

，∴a₁=

3

…（4分）
（Ⅱ）函数y=

3

sin（

π

4

x+?），|?|＜π的一部分图象如图所示，
M（-1，

3

），N(3，-

3

)为图象上的两点，
∴

π

4

×(-1)+?=

π

2

，?=

3π

4

．
∵点MN在函数MN的图象上，如图，连接MN，∠MPN=β，
在△MPN中，由余弦定理得
cosβ=

|PM|2+|PN|2-|MN|2

2|PM||PN|

=

4+12-28

8 3

=-

3

2

，
又∵0≤β≤π∴β=

5

6

π…（9分）
∴?-β=

3π

4

-

5π

6

=-

π

12

∴tan(?-β)=-tan

π

12

=-tan(

π

4

-

π

6

)=-

tan π 4 -tan π 6

1+tan π 4 tan π 6

=-2+

3

…（12分）

点评：本题考查余弦定理的应用两角和与差的正切函数，三角函数的解析式的求法，考查计算能力，转化思想．