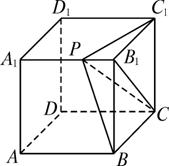
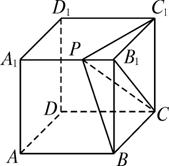
题目内容
如图在棱长为4的正方体ABCD—A1B(1)求直线AP与平面BCC1B1所成的角的大小;
(2)设O点在平面D1AP上的射影是H,求证D1H⊥AP;
(3)求点P到平面ABD1的距离.

(1)解:连接BP,AB⊥平面BCC1B1,BP![]() 平面BCC1B1,
平面BCC1B1,

∴AB⊥BP,α为所求的角的平面角,在Rt△ABP中,BP=![]() ,
,
tanα=![]() ,∴α=arctan
,∴α=arctan![]() .
.
(2)证明:连接D1B1,A
∴D1B1⊥平面A1APC1.AP![]() 平面A1APC1,
平面A1APC1,
∴D1B1⊥AP,
又O在平面D1AP上的射影是H,
∴OH⊥平面D1AP.
AP![]() 平面D1AP,即OH⊥AP,得到AP⊥平面D1OH,D1H
平面D1AP,即OH⊥AP,得到AP⊥平面D1OH,D1H![]() 平面D1OH,
平面D1OH,
∴AP⊥D1H.
(3)解:在平面CC1D1D上作PN∥CD,CD∥AB,得PN∥AB,∴PN∥平面ABD1.
要求P点到平面ABD1的距离,即是求N点到平面ABD1的距离,过N点作NM⊥AD1,垂足为M.
在△ADD1中,AD1=![]() ,ND1=3,
,ND1=3,
∴![]()
![]()
![]() ,NM=
,NM=![]() .
.
∴点P到平面ABD1的距离是![]() .
.

练习册系列答案
相关题目