题目内容
已知函数y=(sinx+cosx)2+2cos2x.(1)求它的递减区间;
(2)求它的最大值和最小值.
分析:首先利用公式把函数y=(sinx+cosx)2+2cos2x转化为y=Asin(ωx+φ)+B的基本形式;
(1)由正弦函数的递减区间求之;(2)由正弦的最大值和最小值求之.
(1)由正弦函数的递减区间求之;(2)由正弦的最大值和最小值求之.
解答:解:y=(sinx+cosx)2+2cos2x
=1+sin2x+1+cos2x
=2+
sin(2x+
)
(1)由
+2kπ≤2x+
≤
π+2kπ(k∈Z)
得
+kπ≤x≤
π+kπ(k∈Z)
所以f(x)的递减区间为[
+kπ,
π+kπ](k∈Z)
(2)f(x)的最大值为2+
,最小值为2-
.
=1+sin2x+1+cos2x
=2+
| 2 |
| π |
| 4 |
(1)由
| π |
| 2 |
| π |
| 4 |
| 3 |
| 2 |
得
| π |
| 8 |
| 5 |
| 8 |
所以f(x)的递减区间为[
| π |
| 8 |
| 5 |
| 8 |
(2)f(x)的最大值为2+
| 2 |
| 2 |
点评:本题主要考查正余弦的倍角公式及形如y=Asin(ωx+φ)+B的函数的性质.

练习册系列答案
相关题目
 的部分图象如图所( )
的部分图象如图所( )
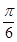 B.ω=1,φ=-
B.ω=1,φ=-