题目内容
如图,在正四棱台内,以小底为底面.大底面中心为顶点作一内接棱锥.已知棱台小底面边长为b,大底面边长为a,并且棱台的侧面积与内接棱锥的侧面面积相等,求这个棱锥的高,并指出有解的条件.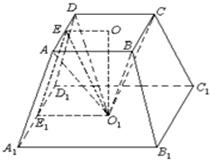

如图,过高OO1和AD的中点E作棱锥和棱台的截面,得棱台的斜高EE1和棱锥的斜高为EO1,设OO1=h,∴S锥侧=
•4b•EO1=2bEO1
S台侧=
(4a+4b)•EE1=2(a+b)•EE1, ∴2bEO1=2(a+b) EE1 ①
∵OO1E1E是直角梯形,其中OE=
,O1E1=
∴根据勾股定理得,EE12=h2+(
-
)2,EO12=h2+(
)2 ②
①式两边平方,把②代入得:b2(h2+
)=(a+b)2[h2+(
-
)2]
解得h2=
,即h=
显然,由于a>0,b>0,所以此题当且仅当a<
b时才有解.
| 1 |
| 2 |
S台侧=
| 1 |
| 2 |
∵OO1E1E是直角梯形,其中OE=
| b |
| 2 |
| a |
| 2 |
∴根据勾股定理得,EE12=h2+(
| a |
| 2 |
| b |
| 2 |
| b |
| 2 |
①式两边平方,把②代入得:b2(h2+
| b2 |
| 4 |
| a |
| 2 |
| b |
| 2 |
解得h2=
| a2(2b2-a2) |
| 4a(a+2b) |
| 1 |
| 2 |
|
显然,由于a>0,b>0,所以此题当且仅当a<
| 2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
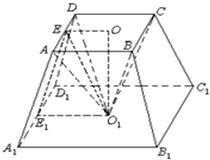 如图,在正四棱台内,以小底为底面.大底面中心为顶点作一内接棱锥.已知棱台小底面边长为b,大底面边长为a,并且棱台的侧面积与内接棱锥的侧面面积相等,求这个棱锥的高,并指出有解的条件.
如图,在正四棱台内,以小底为底面.大底面中心为顶点作一内接棱锥.已知棱台小底面边长为b,大底面边长为a,并且棱台的侧面积与内接棱锥的侧面面积相等,求这个棱锥的高,并指出有解的条件.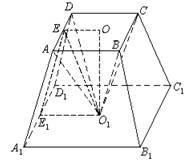
 如图,在正四棱台内,以小底为底面.大底面中心为顶点作一内接棱锥.已知棱台小底面边长为b,大底面边长为a,并且棱台的侧面积与内接棱锥的侧面面积相等,求这个棱锥的高,并指出有解的条件.
如图,在正四棱台内,以小底为底面.大底面中心为顶点作一内接棱锥.已知棱台小底面边长为b,大底面边长为a,并且棱台的侧面积与内接棱锥的侧面面积相等,求这个棱锥的高,并指出有解的条件.