题目内容
若实数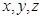 满足
满足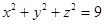 ,则
,则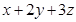 的最大值是 .
的最大值是 .
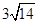
解析试题分析:由柯西不等式得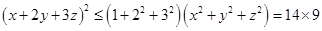 ,故
,故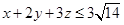 ,所以
,所以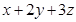 的最大值是
的最大值是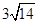 .
.
考点:不等式选讲.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如果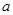 、
、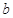 、
、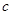 、
、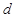 是任意实数
是任意实数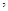 则( )
则( )
A.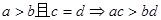 | B.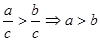 |
C.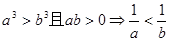 | D.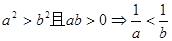 |
题目内容
若实数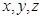 满足
满足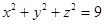 ,则
,则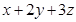 的最大值是 .
的最大值是 .
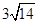
解析试题分析:由柯西不等式得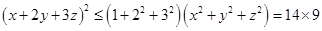 ,故
,故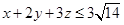 ,所以
,所以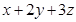 的最大值是
的最大值是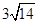 .
.
考点:不等式选讲.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案如果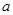 、
、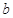 、
、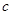 、
、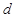 是任意实数
是任意实数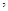 则( )
则( )
A.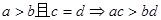 | B.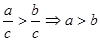 |
C.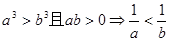 | D.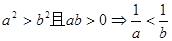 |